
Pythagoras erweitertÄhnliche Figuren an den 3 Seiten eines rechtwinkligen Dreiecks
|
|
0 |
Inhaltsverzeichnis
- Wie lautet der erweiterte Satz des Pythagoras? Was genau besagt er? A1
- Beweis: Warum gilt der erweiterte Satz des Pythagoras? A2
- Welche Beispiele für den erweiterten Satz des Pythagoras findet man im Netz? A3
- 12 Fragen zum Erweiterten Satz des Pythagoras A4
- 1.1 -Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form? A411
- 1.2 -Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form? Sonderfall Parallelogramm A412
- 1.3 -Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form? Sonderfall Tangram A413
- 2-Gilt der Satz des Pythagoras nur für Figuren mit der Fläche "Grundseite ins Quadrat"?"? A42
- 3-Gilt der erweiterte Satz nur für 3 ähnliche Figuren? A43
- 4-Gilt der erweiterte Satz nur für Figuren, die direkt an den Seiten eines rechtwinkligen Dreiecks anliegen? A44
- 5.1-Müssen die Figuren eckig sein? A451
- 5.2-Müssen die Figuren symmetrisch zur Mittel-Senkrechten sein? A452
- 6-Gilt der erweiterte Satz nur für regelmäßige Vielecke? A46
- 7-Ist der Bezug zur Dreiecksseite auf eine best. Stelle in der Figur beschränkt? A47
- 8-Müssen die Flächen nach außen stehen? Dürfen sie auch nach innen stehen? A48
- 9-Dürfen die Flächen sich überschneiden? A49
- 10-Dürfen die Flächen "Löcher" haben? A410
- 11-Gilt er auch für mehrere Figuren pro Seite? A411
- 12-Müssen die Flächen zusammenhängend sein? A412
- Visuelle Beweise für den erweiterten Satz A51
- Pythagoras: Beweise vs. Bestätigungen A52
- Bei welchen Figuren gilt die Erweiterung nicht? A6
- Pythagoras-Baum aus anderen Figuren A71
- Multipler Pythagoras: Ketten von rechtwinkligen Dreiecken A721
- Multipler Pythagoras: Theodorus-Spirale A7221
- Multipler Pythagoras: Zerlegungs-Beweise anhand einer Theodorus-Spirale A7222
- Multipler Pythagoras: 3-Stern und Torpedos A723
- Multipler Pythagoras: Wenn eine Kathete jeweils um 1 LE länger wirdA724
- Multipler Pythagoras: Flächengleichheit mehrerer Ketten von rechtwinkligen Dreiecken A73
- Pythagoras: Flächengleichheit über Kreuz im 4-Eck A74
- Pythagoras: Flächengleichheit über Kreuz im 3-Eck A75
- Pythagoras: Flächengleichheit bei Figurenketten an den 3 Seiten eines 3-Ecks A76
- Pythagoras-Mund A77
- Pythagoras: Flächenverhältnisse bei einem 3-Eck mit eingeschriebenen Quadraten A78
- Quellen A8
|
|
1 |
Wie lautet der erweiterte Satz des Pythagoras? Was genau besagt er?
Der einfache Satz des Pythagoras lautet: Für ein rechtwinkliges Dreieck mit den Katheten a und b und der Hypotenuse c gilt:
a² + b² = c²
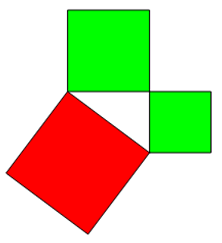
Dieser Satz lässt sich visualisieren, indem man an den 3 Seiten eines rechtwinkligen Dreiecks Quadrate zeichnet. Dabei gilt:
Die Fläche der beiden Quadrate an den beiden kurzen Seiten (den Katheten) ist gleich der Fläche des großen Quadrats an der
längsten Seite (der Hypotenuse).
Der erweiterte (oder auch verallgemeinerte) Satz lautet:
Errichtet man in einem rechtwinkligen Dreieck über den 3 Seiten beliebige zueinander ähnliche Figuren, dann gilt:
Die Summe der Flächeninhalte der Figuren über den Kathetenseiten ist gleich dem Flächeninhalt der Figur über der Hypotenuse.
Springende Punkte liegen bei den Formulierungen "beliebige", "zueinander ähnlich" und "über".
Der erweiterte Satz des Pythagoras ist weitgehend unbekannt.
Nicht-Mathematiker würden Figuren als ähnlich bezeichnen, die "in bestimmten Merkmalen übereinstimmend", "zum Teil übereinstimmend, annähernd gleich"
(duden.de, Duden Bedeutungswörterbuch, 1985) sind.
Mathematiker sehen den Begriff dagegen viel enger. Für sie müssen alle Winkel gleich sein und einander entsprechende
Strecken zueinander proportional sein. Bilder sind im mathematischen Sinne nur dann ähnlich,
wenn sie maßstabsgerechte Vergrößerungen oder Verkleinerungen sind. Würden für einen Nichtmathematiker Rechtecke
der Maße 4x8 und 8x15 ähnlich sein, würde der Mathematiker das nur von Rechtecken
der Maße 4x8 und 8x16 (oder 4x7,5 und 8x15) sagen. Die Übereinstimmung in einer Dimension reicht also für eine
mathematische Ähnlichkeit nicht aus, beiden Dimensionen müssen sich proportional verhalten.
Unscharf ist die Formulierung "über den Seiten" oder "on the three sides". Es geht daraus nicht präzise hervor,
wie genau die Seiten des rechtwinkligen Dreiecks in Beziehung zu den Figuren stehen müssen. Eine Möglichkeit wäre,
dass jede Seite des rechtwinkligen Dreiecks ebenfalls die Seite einer Figur sein muss. Dass dies nicht der Fall ist,
wird weiter unten diskutiert. Im Fall der Volksenzyklopädie Wikipedia sieht man das schon daran, dass in der
deutschen Version zu Recht Kreise als Beispiele herangezogen werden, die natürlich keine Geraden als Seiten haben
(während das bei Halb- oder Viertelkreisen der Fall ist).
|
|
2 |
Beweis: Warum gilt der erweiterte Satz des Pythagoras?
Der Satz des Pythagoras ist eine Gleichung. Gleichungen dürfen umgeformt werden, ohne dass ihr Wahrheitsgehalt sich ändert.[]
Äquivalenzumformungen können insbesondere mit Hilfe von Addition (Subtraktion), Multiplikation (Division) und Potenzierung vorgenommen werden.
Der Satz des Pythagoras besteht auf der linken Seite der Gleichung aus einer Summe mit 2 Elementen. Wenn man auf beiden Seiten der
Gleichung etwas addiert, weiß man nicht, wie der Summand auf die beiden Elemente aufgeteilt werden soll. Wenn man
beide Seiten der Gleichung potenziert, dann verkompliziert sich der Ausdruck auf der Kathetenseite der Gleichung.
Die Multiplikation hat für den Satz des Pythagoras dagegen eine hilfreiche Konsequenz: Bei einer Multiplikation werden die beiden
Summanden einfach mit dem gleichen Faktor multipliziert. Wenn man den Multiplikationsfaktor k nennt, wird der Satz des Pythagoras
wie folgt umgeformt:
a² + b² = c² | *k
k*a² + k*b² = k*c²
Für eine Division gilt das Gleiche. Da jede Division auch als Multiplikation mit dem Kehrwert dargestellt werden kann,
steht k dann für den Kehrwert. "geteilt durch 2" ist identisch mit "multipliziert mit 0,5". In diesem Beispiel wäre k = 0,5.
Dass die Erweiterung um den Faktor k so gut funktioniert, haben wir dem Distributivgesetz zu verdanken: (a+b)*c = a*c + b*c
|
|
3 |
Welche Beispiele für den erweiterten Satz des Pythagoras findet man im Netz?
Der verallgemeinerte Satz des Pythagoras bezieht sich auf beliebige ähnliche Gebilde. Im Netz findet man jedoch keine
beliebigen Figuren, sondern best. Figuren sind überrepräsentiert. Eine einfache Auszählung von 53 Quellen aus dem Netz ergab:
55%: 3-Ecke, 34%: Halbkreise, 32%: regelmäßige 6-Ecke 28%: regelmäßige 5-Ecke
Gründe für die mangelnde Variabilität mögen sein: 1.) Wer abkupfert, spart Zeit und Mühe und kann sicher gehen, dass er keinen
Fehler macht. 2.) Das Naheliegende ist leichter verständlich. Bei Phantasiegebilden ist ein Flächenbeweis schwer zu führen.
3.) Kreativität ist nicht die Stärke von Mathematikern. 4.) Programme wie GEOGEBRA bieten Vielecke standardmäßig an.
Aber es gibt auch "exotische" Beispiele für die "beliebigen ähnlichen Objekte":
verschiedene Bilder (Mona Lisa, Nilpferd, Kaninchen, weitere Tierbilder), bizarre Phantasiefiguren. 3 Bilder von Nilpferden
findet man vermutlich aus folgendem Grund des öfteren: Nilpferd heißt auf Englisch "hippopotamus". Dies Wort klingt ähnlich
wie das Wort "Hypotenuse", das Wort für die lange Seite in einem rechtwinkligen Dreieck. Es handelt sich also um einen Kalauer,
ein Wortspiel. Das Wortspiel ist jedoch nur begrenzt angebracht, da ja auch über den beiden Katheten Bilder des Nilpferdes
zu sehen sind.
Für manche Autoren scheint das Bild eines Hauses mit Dach schon verwegen zu sein.
Eine Aufgabe der vorliegenden Seite besteht darin, die "beliebigen" Flächen etwas systematischer zu explorieren.
|
|
4 |
12 Fragen zum erweiterten Satz des Pythagoras
Die 12 Fragen befassen sich jeweils mit einem Aspekt zum verallgemeinerten Satz. Dabei kommt es immer einmal vor, dass
in einer Beispiels-Grafik Aspekte vorweggenommen werden, die erst in einem späteren Kapitel problematisiert werden.
Wenn Sie das unerträglich finden, lesen Sie einfach nicht weiter!
|
|
4.1.1 |
Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form?
Der Satz des Pythagoras wird normalerweise zur Berechnung fehlender Seiten in einem rechtwinkligen Dreieck angewandt.
Die Abwandlung über Flächen am rechtwinkligen Dreieck dienen a) zur geometrischen Beweisführung und b) der geometrischen Visualisierung,
der Veranschaulichung des Satzes des Pythagoras.
Die Beziehung der Flächen zueinander gilt auch bei Nicht-Quadraten. Sehen wir uns das an Beispielen an, bei denen gilt: die
Flächen sind gleich (also Grundseite ins Quadrat), die Formen sind anders (also keine Quadrate).
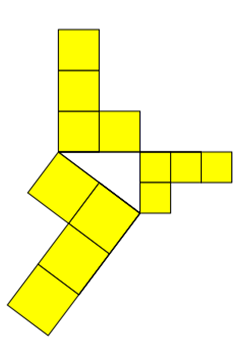
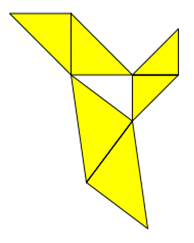

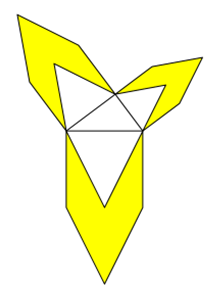
Wenn die Flächen gleich, aber die Formen unterschiedlich sind, kann man auch verschiedene Objekte um das pythagoräische
rechtwinklige Dreieck herumdrapieren.

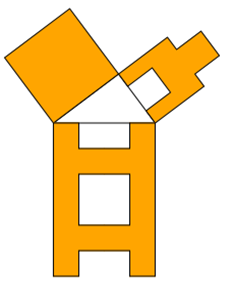
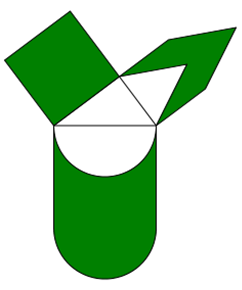
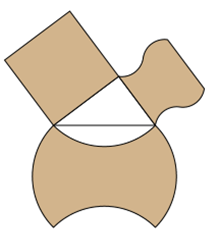
Aufgabe: Konzipieren Sie weitere Formen, die die gleiche Grundseite und Fläche haben wie ein Quadrat, schreiben Sie
ein Programm dafür und ordnen 3 Formen um ein rechtwinkliges Quadrat an!
|
|
4.1.2 |
Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form? Sonderfall Parallelogramm
Die Fläche eines Quadrats berechnet sich über Grundseite * Höhe. Wenn wir die Höhe gleich lassen, aus dem Quadrat jedoch
ein Parallelogramm machen, bleibt die Fläche gleich.
Die Figuren sehen dann anders aus, die Flächen sind jedoch gleich.
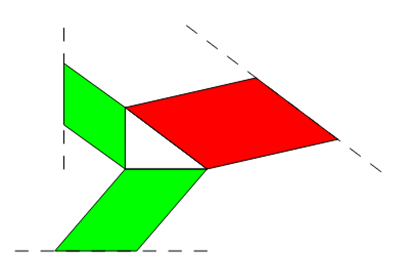
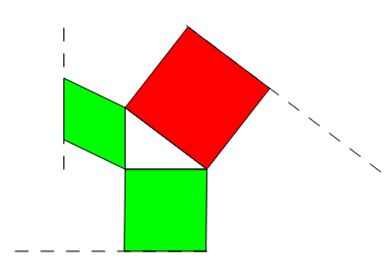
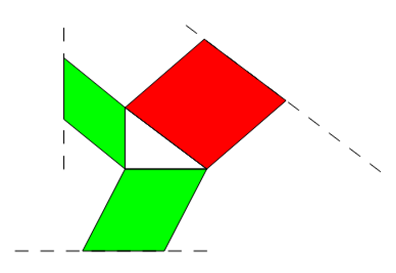
Da die Formen zwar unterschiedlich, die Flächen jedoch gleich sind, darf man in diesem Fall auch verschiedene Formen um
ein rechtwinkliges pythagoräisches Dreieck herumgruppieren. Die Aussage, dass die beiden kleinen Flächen addiert genauso
groß sind wie die Fläche über der Hypotenuse, bleibt wahr, obwohl man nicht auf den ersten Blick sieht, dass die Flächen gleich sind.
Der Fall, dass die Flächen gleich bleiben, aber nicht an den Dreiecksseiten anliegen, wird verhandelt in Abschnitt 4.4.
Dort geht es um Quadrate, man könnte jedoch genauso Parallelogramme nehmen, die nicht an den Dreiecksseiten anliegen.
Aufgabe: Wandeln Sie die Fälle unter 4.4 so ab, dass statt Quadraten Parallelogramme genommen werden!
|
|
4.1.3 |
Gilt der Satz des Pythagoras auch für Objekte mit gleicher Fläche, aber anderer Form? Sonderfall Tangram
Tangram ist ein Legespiel aus 7 Plättchen. Die Plättchen entstehen durch das „Zerschneiden“ eines Quadrates
in zwei große Dreiecke, ein mittelgroßes Dreieck, zwei kleine Dreiecke, ein Quadrat und ein Parallelogramm. Mit diesen
7 Plättchen kann man nicht nur das Ursprungs-Quadrat, sondern eine Vielzahl anderer Formen legen, für die gilt: Sie haben
die gleiche Fläche wie das Ausgangs-Quadrat. Dass die Flächen gleich sind, kann man dadurch überprüfen, dass alle 7
Formen vorhanden sind und dass die Grundseite gleich ist.
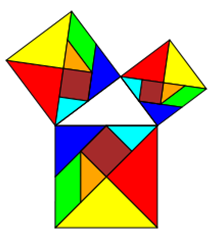
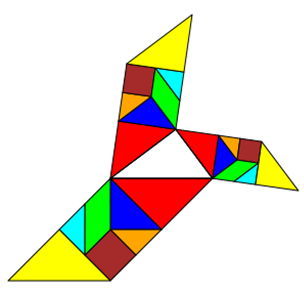
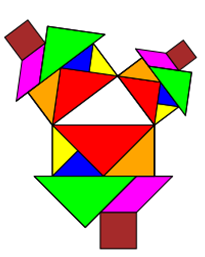
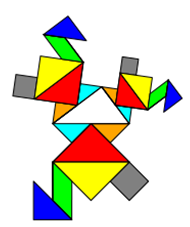
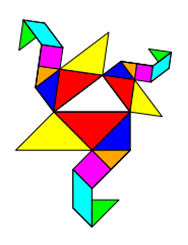
Da die Formen zwar unterschiedlich, die Flächen jedoch gleich sind, darf man in diesem Fall auch verschiedene Formen um
ein rechtwinkliges pythagoräisches Dreieck herumgruppieren. Die Aussage, dass die beiden kleinen Flächen addiert genauso
groß sind wie die Fläche über der Hypotenuse, bleibt wahr, obwohl man nicht auf den ersten Blick (wohl aber auf den zweiten)
sieht, dass die Flächen gleich sind.
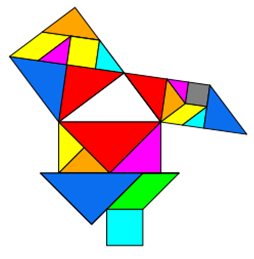
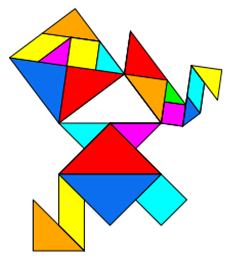
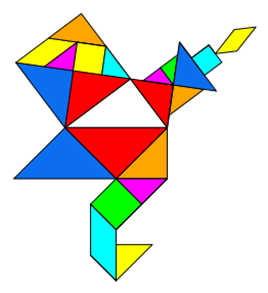
Aufgabe: Konzipieren Sie weitere Tangram-Formen, die die gleiche Grundseite und Fläche haben wie ein Quadrat, schreiben Sie
ein Programm dafür und ordnen 3 Formen um ein rechtwinkliges Quadrat an!
|
|
4.2 |
Gilt der Satz des Pythagoras nur für Figuren mit der Fläche "Grundseite ins Quadrat"?
Nein! Der erweiterte Satz gilt ja für die Flächen k*a², k*b² und k*c². Dabei kann k größer oder kleiner als 1 sein.
Die Flächen sind also immer anders als "Grundseite ins Quadrat", es sei denn k ist gleich 1.
Sehen wir uns einige einfache Fälle an.
Wenn der einfache Satz des Pythagoras mit 2 "erweitert" wird, lautet er 2*a² + 2*b² = 2*c²
Diese Variante lässt sich wie folgt illustrieren.
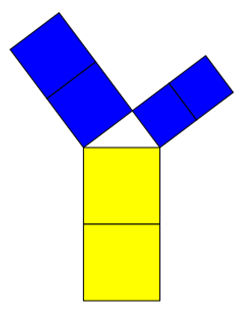
Wenn man jeweils zweieinhalb Quadrate nimmt, lautet er: 2.5*a² + 2.5*b² = 2.5*c²
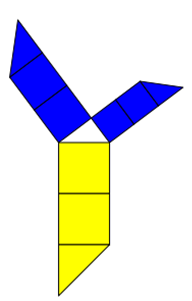
Wenn man jeweils ein Quadrat und ein Viertel Quadrat nimmt, lautet er: 1.25*a² + 1.25*b² = 1.25*c²
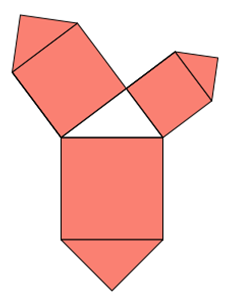
Es folgt ein Beispiel mit einem griechischen Kreuz. Das Kreuz besteht auf 5 Quadraten. Der erweiterte Satz des Pythagoras lautet also in
diesem Fall:
5*a² + 5*b² = 5*c²

Aufgabe: Skizzieren und programmieren Sie weitere "einfache" Beispiele, z.B. mit 3 oder 4 Quadraten!
|
|
4.3 |
Gilt der erweiterte Satz nur für 3 ähnliche Figuren?
Der erweiterte Satz gilt für 3 ähnliche Figuren, dessen Flächen im Verhältnis von a² : b² :c² in einem rechtwinkligen
Dreieck stehen. Solange diese Bedingung erfüllt ist, können die Figuren sich jedoch auch völlig unähnlich sein.
Im Abschnitt 4.1.1 haben wir das anhand von Tangram-Figuren gezeigt, deren Einzelteile sich ähnlich sind, die aber als
Gesamtfiguren völlig unähnlich sind.
Gibt es noch andere Beispiele?
Bei Tangram ist ein Quadrat in bestimmte Dreiecke, Quadrate und Parallelogramme aufgeteilt. Ein Quadrat lässt sich jedoch
noch auf zahlreiche andere Weisen aufteilen. Beispiele dafür sind die Aufteilungen, die für die optischen Beweise des
Satzes von Pythagoras verwendet werden (Siehe dazu Abschnitt 5). Die Einzelteile lassen sich hier natürlich auch zu anderen,
unähnlichen Figuren
zusammenstellen. Der Satz des Pythagoras bleibt dabei wahr, das Verhältnis der Gesamtflächen zueinander bleibt gleich.
Es ist allerdings nicht mehr auf den ersten Blick zu erkennen, dass die beiden kleinen Figuren die gleiche Fläche haben wie
die große Figur, wie von Pythagoras behauptet.
Es gibt weitere Tangram-ähnliche Beispiele. Ivan Moscovich teilt ein Quadrat in 5 verschiedene Teile auf, aus denen man
andere Formen zusammenstellen kann. Diese kann man zu einem pythagoräischen Dreieck mit 3 unähnlichen Figuren zusammenbauen.
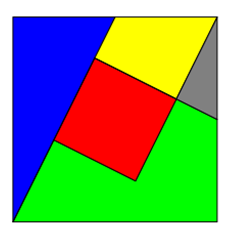
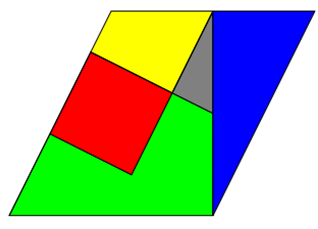
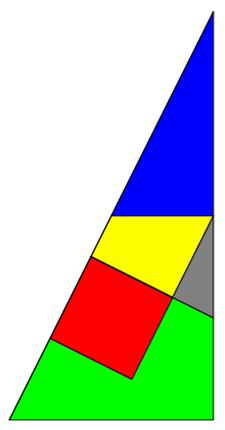
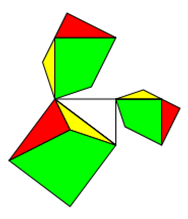
Ähnlich verhält es sich mit dem Quadrat, das man - wie sich Dudenay ausgedacht hat - in die Figur einer Hundehütte
zerlegen kann.
|
|
4.4 |
Gilt der erweiterte Satz nur für Figuren, die direkt an den Seiten eines rechtwinkligen Dreiecks anliegen?
Bei Figuren, die eine Seite mit dem rechtwinkligen Dreieck gemeinsam haben, kann man besonders gut auf den ersten Blick
erkennen, dass die drei Figuren sich proportional zueinander verhalten. Aber sie müssen keine Seite mit dem rechtwinkligen
Dreieck gemeinsam haben. Es genügt, wenn die Figur so konstruiert ist, dass ihre Fläche sich proportional ändert, wenn
sich die Seite des pythagoräischen Dreiecks verändert.
Ein einfaches Beispiel dafür ist ein Quadrat mit der Grundseite des rechtwinkligen Dreiecks, das um eine Ecke herum
gedreht wird.
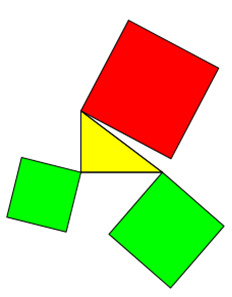
Der Satz des Pythagoras bleibt wahr, wenn die Flächen über den Seiten des rechtwinkligen Dreiecks "schweben".
Dabei ist unerheblich, wo sie sich befinden. Sie können sich in einem proportionalen Abstand von der Grundseite befinden,
müssen das aber keinesfalls.
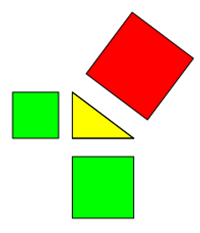
Er bleibt auch wahr, wenn die Objekte nur mit einer Spitze an die Seiten des rechtwinkligen Dreiecks gekoppelt sind.
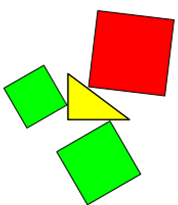
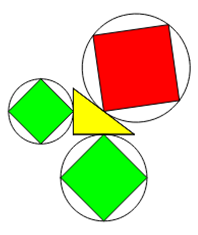
Möndchen haben auch keine Seite mit dem rechtwinkligen Dreieck gemeinsam.
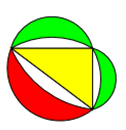
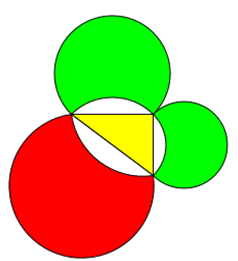
Achtung: Sagen Sie jetzt nicht: "Kenn ich, die Möndchen des Hippokrates." Es handelt sich hier NICHT um die Möndchen des
Hippokrates, sondern um beliebige Möndchen, die auf der einen Seite aus einem beliebigen Kreisbogen und auf der anderen Seite aus einem
kleineren Kreisbogen bestehen. Dabei sind die Winkel der Kreisbögen frei wählbar.
Aufgabe: Suchen Sie weitere Figuren, die nicht die gesamte Seite mit dem pythagoräischen Dreieck gemeinsam haben, sondern nur
die Eckpunkte!
|
|
4.5.1 |
Müssen die Figuren eckig sein?
Nein. Ein Beispiel für eine nicht-nur-eckige Figur, das man häufig im Netz findet, ist der Halbkreis.
Genauso gilt er jedoch auch für einen ganzen Kreis, einen beliebigen Kreissektor oder ein Kreissegment.
Damit die 3 Figuren ähnlich sind, müssen die Winkel gleich sein.
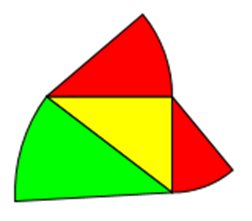
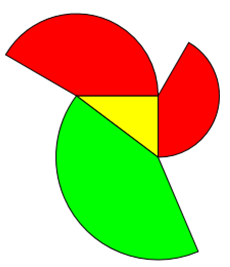
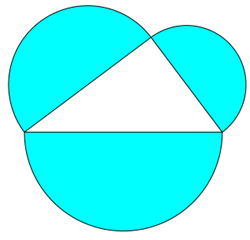
Ein anderes Beispiel ist die Urne. Sie ist gleichzeitig ein Beispiel dafür, dass die Figuren nicht mit einer Seite am
Dreieck liegen müssen, dass Figuren die Flächen a², b² und c² haben können, aber keine Quadrate sind.
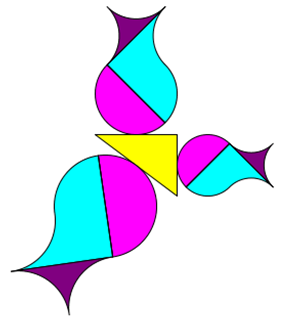
|
|
4.5.2 |
Müssen die Figuren symmetrisch zur Mittel-Senkrechten sein?
Regelmäßige Vielecke und Halbkreise sind symmetrisch zur Mittelsenkrechten.
Der Satz des P. gilt aber auch für unsymmetrische Gebilde.
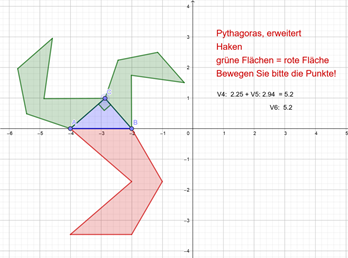
Wenn Sie hier oder auf das Bild klicken
(zur Rückkehr 2x "zurück" klicken und "Seite verlassen"), sehen Sie ein rechtwinkliges Dreieck, umgeben von Haken, von mir programmiert in
Geogebra. Wenn man die Lage von Punkten und damit Größe oder Winkel dynamisch und interaktiv verändert,
so bleibt die Hauptaussage immer bestehen: Die Flächen der kleinen Haken = Fläche des großen Hakens
|
|
4.6 |
Gilt der erweiterte Satz nur für regelmäßige Vielecke?
Die meisten Beispiele für den erweiterten Satz des Pythagoras sind gleichseitige 3-Ecke, 5-Ecke, 6-Ecke und 8-Ecke.
Die werden vermutlich genommen, weil sie leicht zu konstruieren sind und ihre Fläche rel. leicht zu berechnen ist.
Der erweiterte Satz gilt aber nicht nur dafür, sondern für beliebige zueinander ähnliche Figuren.
|
|
4.7 |
Ist der Bezug zur Dreiecksseite auf eine best. Stelle in der Figur beschränkt?
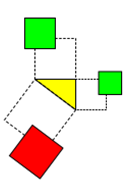
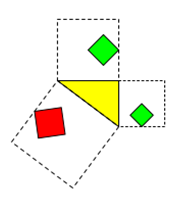
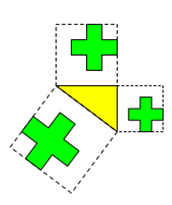
Die anzufindenden Beispiele suggerieren möglicherweise, dass die Figuren eine Seite mit der Seite des
rechtwinkligen Dreiecks gemeinsam haben müssten. Das ist falsch.
Ein Bezug zur Seite des Dreiecks muss bestehen, so dass
die Figur proportional wächst, wenn die Seitenlänge wächst. Dieser Bezug kann aber an einer beliebigen Stelle auftreten.
|
|
4.8 |
Müssen die Flächen nach außen stehen? Dürfen sie auch nach innen stehen?
Ja. Sie können auch gemischt teils nach außen, teils nach innnen stehen. Wenn sie nach innen stehen, ist das Risiko
groß, dass sie sich überschneiden und das Bild dadurch unübersichtlich wird.
Das folgende Bild zeigt Kreisbögen, die auch ein Beispiel für nicht-eckige Figuren (Kapitel 4.5) sind.
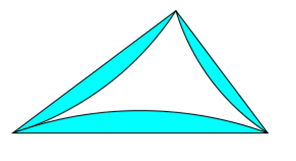
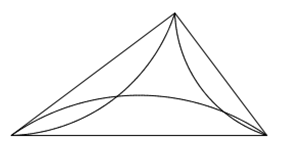
|
|
4.9 |
Dürfen die Flächen sich überschneiden?
Ja. Überschneidungen haben den Nachteil, dass sie unübersichtlich sind. Das gilt umso mehr für gefärbte Flächen.
Im der folgenden Abbildung sieht man 10-Ecke und 12-Ecke, die sich überschneiden. Der Satz des Pythagoras gilt trotzdem.
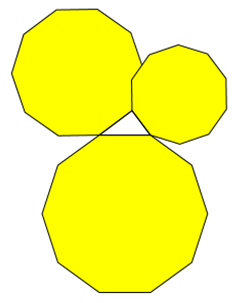
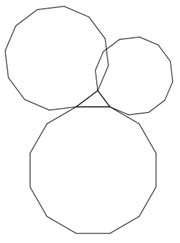
Ein anderes Beispiel findet man im Kapitel 4.9 bei sich überschneidenden Kreisbögen.
|
|
4.10 |
Dürfen die Flächen "Löcher" haben?
Ja, die Flächen dürfen Löcher haben. Natürlich nur, wenn die Gesamtfläche von der jeweiligen Dreieckseite abhängig ist.
Betrachten wir mal den Fall mit einem Quadrat und einem Quadrat mit halber Grundseite als Loch.
Dann gilt für die 3 Quadrate außen und die 3 Lochquadrate:
a² + b² = c²
a²/4 + b²/4 = c²/4
Die Gesamtflächen ergeben sich, wenn man die Lochgleichung von der ersten Gleichung subtrahiert:
a²*3/4 + b²*3/4 = c²*3/4
Wie man sieht, ist die resultierende Gleichung wieder nur eine erweiterte Pythagoras-Gleichung mit dem Faktor k=3/4.
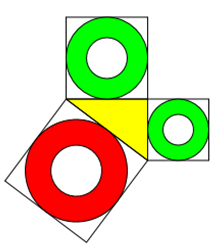
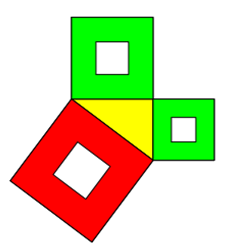
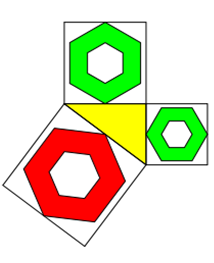
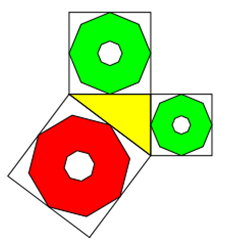
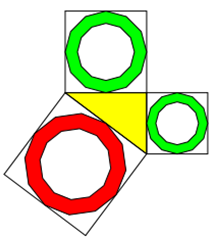
Die Umgebungsquadrate könnten auch weggelassen werden. Sie helfen jedoch bei der Einschätzung, ob die eigentlichen
Objekte von den Grundseiten abhängig sind, d.h. ob sich die Objekte proportional verändern. (Gewisseheit kann einem nur
der Quell-Code verschaffen.)
Aufgabe: Denken Sie sich weitere löcherige Objekte aus, auch solche mit mehreren Löchern und andersgeformten Löchern!
|
|
4.11 |
Gilt er auch für mehrere Figuren pro Seite?
Die Figuren mit Löchern im Kapitel 4.11 können als jeweils 2 Figuren (Außenring und Loch) interpretiert werden.
In den folgenden Abbildungen sind jeweils 3 gleichseitige Dreiecke bzw. 2 Halbkreise zu sehen.
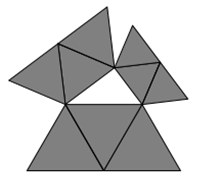
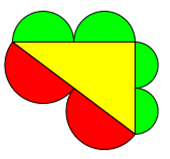
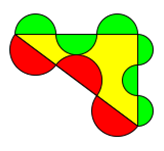
Es ist besonders interessant, dass der Satz des Pythagoras sowohl für die Gesamtfigur, als auch für alle Elemente und
Zusammenfassungen von Elementen gilt.
|
|
4.12 |
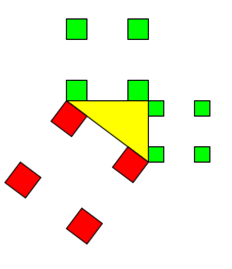
Müssen die Flächen zusammenhängend sein?
Nein! Im Folgenden ein Beispiel mit je 4 Quadraten, die nicht zusammenhängen.
Auch hier gilt, weil die Flächen so programmiert sind, dass sie von der jeweiligen Dreiecks-Grundseite abhängig sind: Die grünen Flächen sind genauso groß wie die roten Flächen.
|
|
5.1 |
Visuelle Beweise für den erweiterten Satz
Es gibt zahlreiche Zerlegungsbeweise für den (normalen) Satz des Pythagoras. Dabei wird ein Quadrat so in Teilflächen zerlegt,
dass man aus diesen Teilen 2 kleinere Quadrate zusammensetzen kann. Der Clou sollte dabei sein, dass die Zerlegung so
flexibel ist, dass verschiedene Quadratsgrößen bei der Zerlegung herauskommen.
Wie wir gesehen haben, gilt der Satz des Pythagoras für beliebige Formen. Man wird vermutlich keine Methode finden,
mit deren Hilfe man beliebige Formen so zerlegen kann, dass dabei 2 ähnliche Formen herauskommen. Aber es wird möglich sein,
Zerlegungsbeweise für best. Formen zu erstellen. Welche Formen bieten sich an, bzw. für welche Formen existieren bereits
Zerlegungsbeweise?
Zerlegung der Figur in ein Quadrat, dann Zerlegung der Quadrate wie bekannt
Hierbei geht man in 2 Schritten vor. Zunächst wird versucht, die Figur so zu zerlegen, dass daraus ein Quadrat gelegt werden kann.
Das bedeutet, dass das Bild mit besonderen Formen in ein Bild mit 3 Quadraten transformiert wird. Für die Quadratform gibt
es bereits diverse Zerlegungsbeweise, die in einem zweiten Schritt durchgeführt werden können.
Eine Zerlegung von gleichseitigen 3-Ecken in Quadrate und umgekehrt wird hier gezeigt.
Zerlegung von gleichseitigen Vielecken in kleinere Vielecke
Es gibt einen spezifischen Zerlegungsbeweis für Vielecke. Man findet ihn u.a. bei Hans Walser,
in der Toolbox Lehrerbildung der TU München,
auf Seiten von Steve Phelps mit Geogebra.
Es bleibt unklar, wer diese Zerlegungsbeweise "erfunden" hat. Alle 3 haben gemeinsam,
dass Details zum making of, d.h. verwendete Software, Winkel und Längen der Teilfiguren, nicht verraten werden.
Die beiden letzteren sind interaktiv und variabel. Sie haben den Vorteil, dass Winkel und Größe des
rechtwinkligen Dreiecks frei wählbar sind. Die Variabilität ist keine Spielerei: Wenn ein mathematisches Gesetz behauptet,
für alle rechtwinkligen Dreiecke zu gelten, dann sollte man das in einem Beweis auch zeigen. Anders ausgedrückt: Es genügt nicht,
sich ein Beispiel herauszupicken, bei dem es funktioniert - es könnte ja sein, dass dieses Beispiel die Ausnahme ist. Die
excellente Geogebra-Seite von Phelps ist so spartanisch-minimalistisch und enthält keine Erläuterungen, dass die Wahrscheinlichtkeit,
dass sie von einer Vielzahl von Interessierten gefunden wird, leider minimal ist. Sie könnte durch Angabe des Winkels und der
Teilflächen optimiert werden.
Der Beweis gilt nicht nur für eine best. Form, sondern eine ganze
Klasse von Formen, nämlich regelmäßige Vielecke.
Dabei wird ein n-Eck so zerlegt, dass in der Mitte ein kleineres
n-Eck bleibt. Der Rest der Fläche wird in n 4-Ecke und n 3-Ecke zerlegt, so dass je ein 4-Eck und ein 3-Eck eine Drachenform
ergeben, die dann ein mittelgroßes n-Eck aus n Drachen bilden.
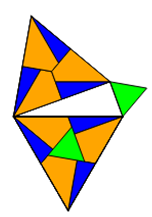
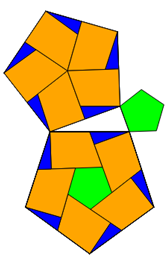
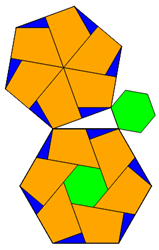
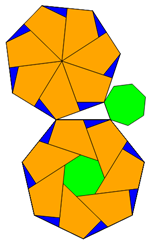
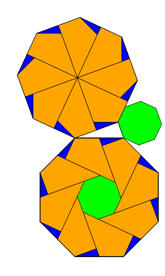
Diese Zerlegungen sind zentristisch und symmetrisch. Das sieht sehr elegant aus und ist rel. einfach, weil nur 3
verschiedene Objekte konstruiert werden müssen. Wenn man sich z.B. den Zerlegungsbeweis für Quadrate am
rechtwinkligen Dreieck von Marcus Girbert ansieht und die Zerlegung
anzeigen lässt, sieht man, dass Zerlegungen jedoch keineswegs zentristisch und symmetrisch sein müssen. Jetzt liegt der
Verdacht nahe, dass dies nicht nur für 4-Ecke, sondern auch für andere Vielecke gilt.
Im Folgenden zeige ich, dass es für Dreiecke nicht-zentristische Zerlegungen gibt, die als optischer Beweis für
pythagoräische Zusammenhänge bei gleichseitigen Dreiecken taugen.
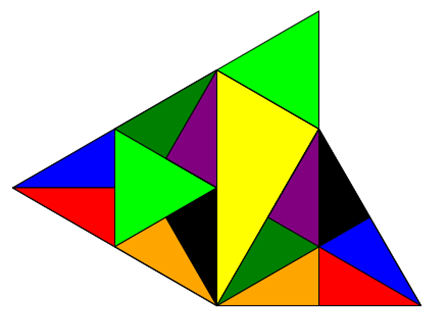
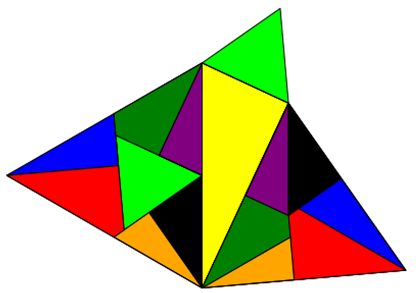
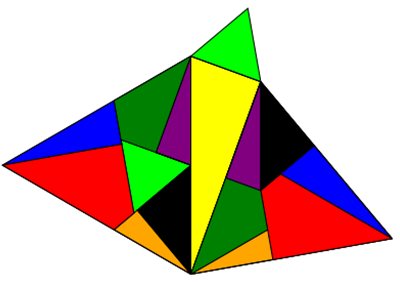
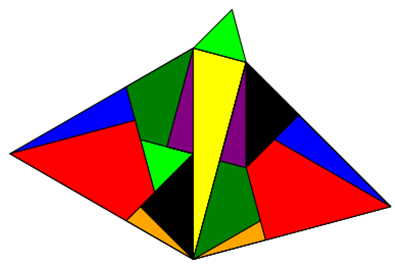
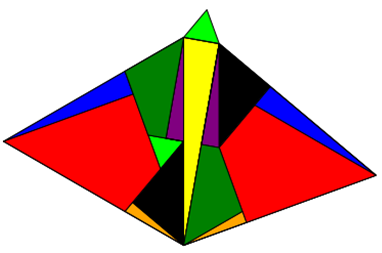
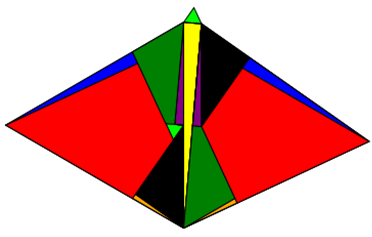
Aufgaben: Zeigen Sie mit Hilfe von Geogebra oder einer ähnlichen Software, dass die gleichseitigen Innendreiecke auf
verschiedenen Positionen, also nicht nur am Rand wie in meinem Beispiel, liegen können. Zeigen Sie, dass nicht-zentristische
Zerlegungen auch für 5-Ecke, 6-Ecke usw. existieren! (Wäre das eine Aufgabe für JUGEND FORSCHT?)
Ein feiner visueller Beweis des Satzes des Pythagoras mit gleichseitigen Dreiecken mit Ergänzungen und Scherungen findet sich hier.
Folgende Zerlegungs- bzw. Scherungsbeweise finden sich für best. Figuren:
Aufgabe: Finden Sie weitere Zerlegungsbeweise für die o.g. Formen sowie Zerlegungsbeweise für weitere andere Formen!
|
|
5.2 |
Pythagoras: Beweise vs. Bestätigungen
Sätze wie der Satz des Pythagoras gelten für unendlich viele verschiedene Fälle. Wenn das richtig ist, muss auch bewiesen
werden, dass genau das der Fall ist: dass er für alle möglichen verschiedenen Fälle gilt. Umgekehrt: Wenn man zeigt, dass
Pythagoras für bestimmte rechtwinklige Dreiecke (z.B. gleichschenklige) gilt, dann hat man damit noch nicht bewiesen, dass es für alle möglichen
rechtwinkligen Dreiecke gilt.
Beispiele:
- Das folgende Beispiel zeigt anhand einer Zerlegung, dass der Satz des Pythagoras auch für gleichseitige Dreiecke gilt.
Die Zerlegung funktioniert hier jedoch nur für die Konstellation 17LE:15LE:8LE. Die Zerlegung beweist also nicht, ob der Satz
des Pythagoras auch für gleichseitige Dreiecke mit anderen Längen-Verhältnissen gilt.
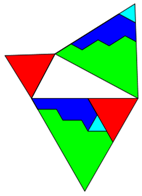
- Das folgende Beispiel zeigt anhand einer Zerlegung, dass der Satz des Pythagoras auch für lateinische Kreuze gilt.
Die Zerlegung funktioniert hier jedoch nur für rechtwinklige gleichseitige Dreiecke. Die Zerlegung sagt also nichts darüber
aus, ob der Satz des Pythagoras auch für lateinische Kreuze um andere rechtwinklige Dreiecke herum gilt. Die Beweiskraft dieser
Zerlegung ist also sehr gering.
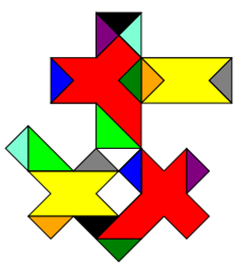
- Wenn man mit Hilfe von Zerlegung in kleine Quadrate zeigt, dass Pythagoras für das Tripel (3LE)²+(4LE)²=(5LE)² gilt, dann ist das
eine eindrucksvolle Bestätigung des Satzes, aber eben nur ein gültiger Spezialfall.
- Wenn man mit Hilfe von Zerlegung in kleine gleichseitige Dreiecke zeigt, dass Pythagoras für gleichseitige Dreiecke
und das Tripel 3-4-5 gilt, dann ist das eine eindrucksvolle Bestätigung des Satzes, sagt aber nichts darüber aus, ob es auch
für alle Arten von rechtwinkligen Dreiecken gilt.
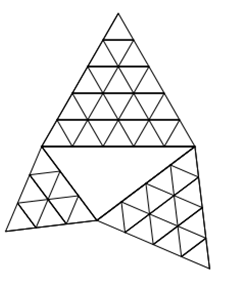
-
Auch in diesem Fall gilt die Zerlegung nur für bestimmte Maße, ist also kein allgemeiner Beweis.
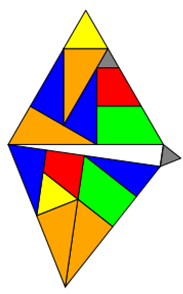
- Die hier
vorgeführten Zerlegungen von gleichseitigen 3-Ecken und 6-Ecken (und Quadraten) gelten nur
für ein rechtwinkliges Dreieck mit den Seitenverhältnissen 3:4:5. Es handelt sich also keinesfalls um einen "proof" of the
"incredible theorem of Pythagoras".
- Das hier präsentierte "Puzle triangular" ist eine Zerlegung, die nur für ein bestimmtes rechtwinkliges Dreieck
(Seitenverhältnis 1 : sqrt(3) : 2) möglich ist. Seine Beweiskraft ist also nur sehr klein.
- Ähnliches gilt - bitte zeigen! - vermutlich für die Trapez-Zerlegung und die Treppen-Zerlegung (ibidem).
Ihre Beweiskraft gilt also 1.) nur für best. Figuren und 2.) nur für bestimmte Seitenverhältnisse.
- Ein Zerlegungsbeweis für Pythagoras mit gleichseitigen Dreiecken beweist, dass er für gleichseitige Dreiecke gilt. Es ist
jedoch nur eine Bestätigung des viel allgemeineren Satzes, der für alle beliebigen Figuren Gültigkeit beansprucht.
Die Beweiskraft von interaktiven Pythagoras-Figuren ist viel größer als die von statischen Bildern, wenn a) die Winkel
des rechtwinkligen Dreiecks beliebig variiert werden können, b) die Größe und c) die Art der angeschlossenen Figuren.
Ergo: Checken Sie genau, was Ihnen als "Beweis" verkauft wird - vielleicht ist es lediglich ein positiver Einzelfall, also
eine kleine Bestätigung. Glauben Sie nicht an "induktive Beweise" nach dem Motto "Hat man einen Fall bestätigt, hat man
alle bewiesen.". Allgemeingültige Beweise lassen sich nicht so leicht finden wie im "Tatort".
|
|
6 |
Bei welchen Figuren gilt die Erweiterung nicht?
Die Flächengleichkeit gilt nicht, wenn man wahllos 3 verschiedene Figuren um ein rechtwinkliges 3-Eck drapiert.
Die folgenden Sätze stimmen leider nicht:
a³+b³=c³
a^4+b^4=c^4
Heißt das, dass Pythagoras in der dritten Dimension nicht anwendbar ist?
Doch, Pythagoras ist durchaus in der dritten Dimension anwendbar. Und zwar, wenn die dritte Dimension ein konstanter Faktor
wie beim ertweiterten Satz ist.
Wenn wir also aus den 3 Quadraten 3 Quader machen, indem wir die Quadrate um den Faktor k LE in die Höhe bauen, dann gilt:
ka²+kb²=kc²
Aus diesem Grund sind auch die eindrucksvollen Flüssigkeitsbeweise korrekt (Siehe z.B. hier oder hier).
Analog wären Flüssigkeits"beweise" mit dreidimensionalen Dreiecken, Halbkreisen usw. zulässig.
|
|
7.1 |
Pythagoras-Baum aus anderen Figuren
Bei einem Pythagoras-Baum wird an ein Quadrat ein
rechtwinkliges Dreieck mit den dazugehörigen Quadraten angesetzt. Dieses
Verfahren wird rekursiv wiederholt, so dass ein Gebilde entsteht, das einem Baum ähnelt.
Dies funktioniert auch, wenn man anstelle von Quadraten andere Formen verwendet.
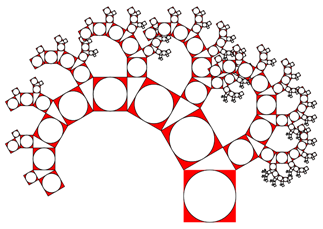
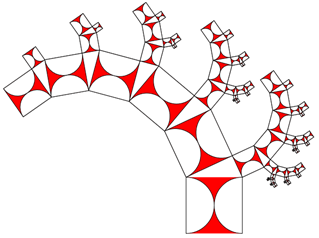

Das funktioniert nicht nur mit kompletten Bäumen, sondern auch mit einzelnen eingerollten Ästen oder Rechts-Links-Ästen.
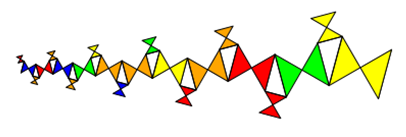

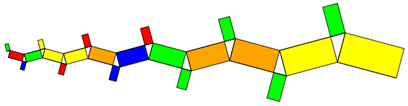
Aufgabe: Finden Sie weitere Pythagoras-Bäume/-Äste!
|
|
7.2.1 |
Multipler Pythagoras: Ketten von rechtwinkligen Dreiecken
Bei der Illustration des einfachen Satzes des Pythagoras sieht man ein
rechtwinkliges Dreieck mit 3 Figuren über den 3 Seiten.
Es können jedoch auch mehrere rechtwinklige Dreiecke hintereinandergeschaltet werden, mit Quadraten an den Seiten.
Dabei gilt:
Die Summe der Flächen über den Katheten ist gleich der Fläche über der Hypotenuse.
Das gilt nicht nur für Quadrate, sondern auch für beliebige andere Flächen, sofern sie proportional zu den Seiten sind.
Es können beliebig viele Dreiecke miteinander verkettet werden.
Es kann dabei leicht zu Überschneidungen kommen. Flächen, die sich überschneiden, sehen natürlich nicht so elegant und
übersichtlich aus. Die Wahrheit des Satzes wird dadurch jedoch nicht beeinträchtigt.
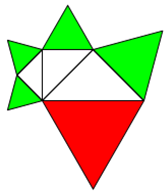
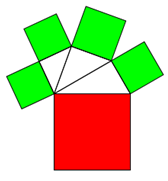
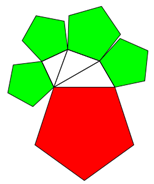
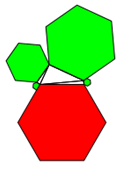
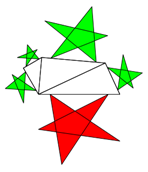
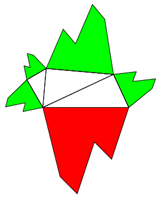
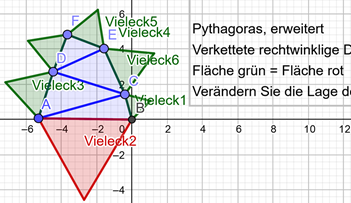
Wenn Sie hier oder auf das Bild klicken
(zur Rückkehr 2x "zurück" klicken und "Seite verlassen"), sehen Sie eine Verkettung von Dreiecken, von yours truly programmiert in
Geogebra. Wenn man die Lage von Punkten und damit Größe oder Winkel dynamisch und interaktiv verändert,
so bleibt die Hauptaussage immer bestehen: Die Flächen der kleinen gleichseitigen 3-Ecke = Fläche des großen, roten 3-Ecks
Aufgabe: Verketten Sie rechtwinklige Dreiecke auf andere Weise und setzen Sie andere Figuren an die Seiten!
|
|
7.2.2.1 |
Multipler Pythagoras: Theodorus-Spirale
Bei einer Theodorus-Spirale
(auch Wurzelschnecke, Wurzelspirale genannt, also called square root spiral, Einstein spiral, or Pythagorean spiral)
geht man von einem gleichschenkligen rechtwinkligen Dreieck
mit Schenkellänge 1 Einheit aus. An die Hypotenuse werden weitere rechtwinklige Dreiecke angefügt,
deren Kathete ebenfalls eine Einheit lang ist. Die Hypotenusen haben dann eine Länge von Wurzel aus 2, Wurzel aus 3 usw..
Um die Seitenlängen zu veranschaulichen, kann man jeweils Quadrate an sie anlegen. Da es sich jeweils um rechtwinklige
Dreiecke handelt, kann man jedoch auch beliebige andere Figuren verwenden.
Interessante Sonderfälle ergeben sich, wenn die Anzahl der Katheten Quadratzahlen sind. Illustrieren wir dies mit
gleichseitigen Dreiecken.
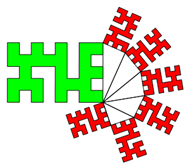
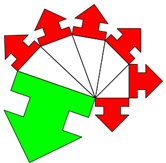
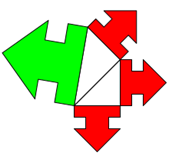
Flächengleichheit von kleinen Figuren vs. großer End-Figur gilt bei beliebiger Anzahl kleiner Figuren.
|
|
7.2.2.2 |
Multipler Pythagoras: Zerlegungs-Beweise anhand einer Theodorus-Spirale
Die Wahrheit von Pythagoras-Ketten kann prinzipiell durch Zerlegungen bewiesen werden. Hier ist ein Zerlegungsbeweis
für eine besondere Verkettung mit angeschlossenen identischen 3-Ecken, deren Fläche in Summe gleich der Fläche des großen
Dreiecks ist.
Die Beweiskraft ist natürlich sehr gering, da die Zerlegung nur mit Quadratzahlen funktioniert.
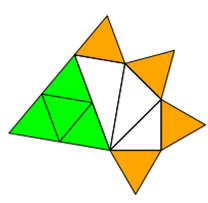
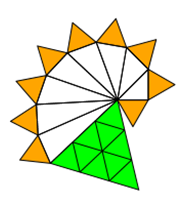
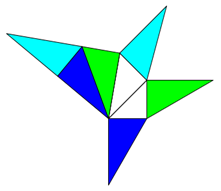
Wie man sehen kann, gilt orange = grün. Bei 16, 25 etc. kleinen Dreiecken stimmt die Beziehung immer noch,
aber es kommt zu unübersichtlichen Überschneidungen.
Flächengleichheit von kleinen Dreiecken vs. großem End-Dreieck gilt bei beliebiger Anzahl kleiner Dreiecke, nur erhält
man dann kein großes Dreieck, das sich in die kleinen Dreiecke zerteilen lässt.
Aufgaben:Finden Sie weitere Zerlegungsbeweise für Pythagoras-Ketten mit Katheten der Länge 1 LE!
Bei Ivan Moscovich, Formenrätsel, S. 41 findet man die Zerlegung eines 5-Sterns in 4 kleinere Sterne gleicher Form.
Bei Ivan Moscovich, Über 500 Brain Games, S. 26 findet man die Zerlegung eines 5-Sterns in 5 kleinere Sterne gleicher Form.
Bei Ivan Moscovich, Formenrätsel, S. 43 findet man die Zerlegung eines 9-Ecks in 3 kleinere 9-Ecke.
Bei Ivan Moscovich, Formenrätsel, S. 44 findet man die Zerlegung eines 12-Sterns in 3 kleinere 12-Sterne.
Bei Ivan Moscovich, Formenrätsel, S. 45 findet man die Zerlegung eines anderen 12-Sterns in 3 kleinere 12-Sterne.
Fündig wird man auch, wenn man nach Rep-tiles (hier klicken!) sucht.
Ein Rep-tile ist eine Form, die in gleiche, kleinere Formen zerlegt werden kann.
Ein Beispiel sieht man oben: das rechtwinklige 3-Eck, das in 3 formgleiche 3-Ecke zerlegt werden kann.
Es finden sich auch Beispiele für eine Zerlegung in 2 oder mehr verschieden große Formen, die man in Pythagoras-Ketten
einbauen könnte!
|
|
7.2.3 |
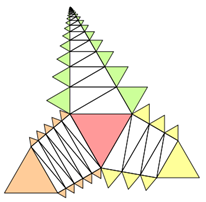
Multipler Pythagoras: 3-Sterne und Torpedos
Man kann mit rechtwinkligen 3-Ecken gleichmäßige Türme bauen, wenn man die rechten Winkel abwechselnd rechts und links
platziert und rechts und links den gleichen Winkel nimmt. Diese Türme können zu 3-Sternen und Torpedos zusammengestellt
werden.
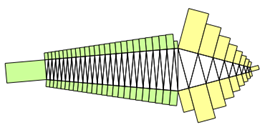
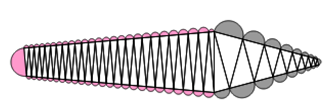
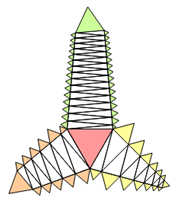
Es gilt jeweils, dass die Seitenflächen verschiedener Farben in Summe die gleiche Fläche haben.
Schiefe Türme, bei denen eine Seite senkrecht steht, lassen sich ähnlich erstellen.
|
|
7.2.4 |
Multipler Pythagoras: Wenn eine Kathete jeweils um 1 LE länger wird
Oben hatten wir uns mit dem Sonderfall befasst, wenn eine Kathete jeweils 1 LE lang ist.
Wie sieht es aus, wenn die Kathete jeweils um 1 LE länger wird?.
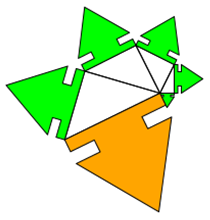
Wenn die Seitenlängen von 1 bis n gehen, dann gehen die Seitenquadrate von 1 bis n². Die Summe der Quadratzahlen
lässt sich über die Formel n(n+1)(2n+1)/6 berechnen.
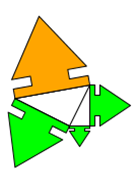
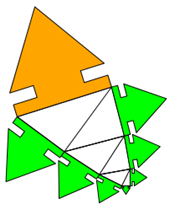
Wenn man die rechtwinklligen 3-Ecke abwechselnd rechts und links anschließt, ergibt sich eine Form, die - im Gegensatz zur Schnecke - keine
Probleme mit Überschneidungen hat.
|
|
7.3 |
Multipler Pythagoras: Flächengleichheit mehrerer Ketten von rechtwinkligen Dreiecken
Man kann auch demonstrieren, dass die Fläche ähnlicher Figuren in Summe gleich ist bei gleicher Hypotenuse.
Die Dreiecksketten können nebeneinander stehen oder sich gegenüber stehen.
Pro Seite können unterschiedliche Anzahlen von Figuren auftreten.
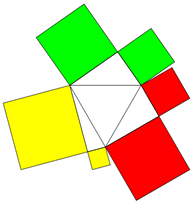
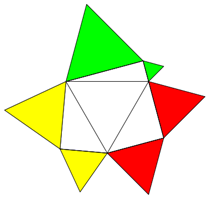
Aufgabe:Verketten Sie 2 und mehr Dreiecke pro Seite!
Aufgabe:Setzen Sie andere Figuren an die Seiten!
|
|
7.4 |
Pythagoras: Flächengleichheit über Kreuz im 4-Eck
Konstruieren Sie ein beliebiges unregelmäßiges 4-Eck, dessen Diagonalen rechtwinklig aufeinander stehen! Man sieht,
dass dieses 4-Eck aus 4 rechtwinkligen 3-Ecken besteht. Das bedeutet, dass hier der Satz des Pythagoras angewendet werden kann.
(Orthodiagonales Viereck)
Wenn die Seiten des 4-Ecks mit a, b, c, d und die Katheten der rechtwinkligen 3-Ecke mit u, v, x, y benannt werden, dann lassen sich laut Pythagoras 4 Gleichungen aufstellen:
a²=u²+y²
c²= x²+v²
b²=y²+v²
d²=x²+u²
Wenn wir je 2 Gleichungen addieren, ergibt sich:
a²+ c²=u²+v²+x²+y²
b²+ d²=u²+v²+x²+y²
Da die beiden rechten Seiten der Gleichung identisch sind, können wir die beiden linken Teile gleichsetzen:
a²+ c²=b²+ d²
Das bedeutet in Worten, dass die Summen der Quadrate von einander gegenüberliegenden Seiten gleich sind. Der Satz lautet also:
Wenn die Diagonalen eines 4-Ecks sich orthogonal schneiden,
dann sind die Summen der Quadrate von sich gegenüberliegenden Seiten genau gleich.
Da 4 mal der Satz des Pythagoras angewandt wurde, könnte man auch 4 mal den erweiterten Satz des Pythagoras anwenden, d.h. den Satz jeweils mit dem Faktor k erweitern.
Man kommt dann zu der Gleichung
ka²+kc²=kb²+ kd²
Das bedeutet wieder, dass man bei der Illustration des Satzes beliebige zueinander ähnliche Figuren einsetzen kann.
Aufgabe: Programmieren Sie in Geogebra oder einem ähnlichen Programm ein 4-Eck, das aus 4 durch Schieberegler frei wählbaren Strecken besteht, die 4 rechtwinklige 3-Ecke bilden. Stellen Sie verschiedene Figuren zur Wahl, die auf die 4 Seiten gesetzt werden und deren Flächen berechnet und angezeigt werden.
Ein Sonderfall liegt vor, wenn y = 0 ist. Dann hat man es statt mit einem 4-Eck mit einem 3-Eck zu tun, auf dessen Hypotenuse ein Lot gefällt ist. Wenn man die beiden Teile der Hypotenuse als p und q bezeichnet, lautet der Satz dann:
p²+ c²=q²+ d² bzw. erweitert
kp²+ kc²=kq²+ kd²
Aufgabe: Leiten Sie diesen Satz auch aus dem Höhensatz des Euklid (h²=pq) und dem Satz des Pythagoras für die beiden kleinen 3-Ecke ab!
Aufgabe: Programmieren Sie in Geogebra oder einem ähnlichen Programm ein durch Schieberegler frei wählbares rechtwinkliges 3-Eck, auf dessen Hypotenuse das Lot gefällt wird. Stellen Sie verschiedene
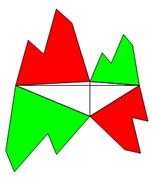
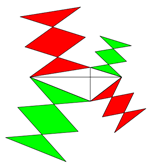
Aufgabe: Programmieren Sie in Geogebra oder einem ähnlichen Programm ein durch Schieberegler frei wählbares
orthodiagonales 4-Eck und setzen auf die 4 Seiten beliebige proportionale Figuren! Zeigen Sie, dass die Summen gegenüberliegender
Flächen gleich sind! Stellen Sie verschiedene Figuren über die Seiten!
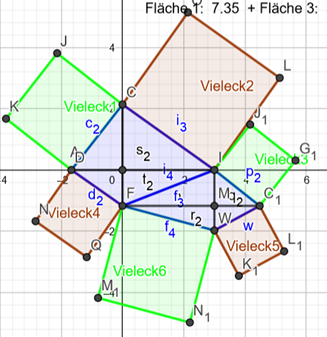
Man kann auch 2 orthodiagonale Vierecke an einer Seite zusammensetzen.
Wenn Sie hier oder auf das Bild klicken
(zur Rückkehr 2x "zurück" klicken und "Seite verlassen"), sehen Sie eine Verkettung von Dreiecken, von yours truly programmiert in
Geogebra. Bei beliebigen Konstellationen mit beliebigen Vielecken gilt die Aussage: Grüne Flächen = braune Flächen, wie man anhand
der Zahlen verfolgen kann.
Aufgabe: Versuchen Sie, über den Satz des Thales 2 orthodiagonale Vierecke flexibler miteinander zu verknüpfen (und das in
Geogebra oder einem ähnlichen Programm zu programmieren), so dass die Orthodiagonalen nicht im gleichen Winkel zueinander stehen.
|
|
7.5 |
Pythagoras: Flächengleichheit über Kreuz im 3-Eck
Konstruieren Sie ein rechtwinkliges Dreieck mit der Höhe auf der Hypotenuse. Die Höhe teilt die Hypotenuse in 2 Strecken,
die beim Höhensatz des Euklid p und q genannt werden.
Man zeichne dann Quadrate über die Katheten sowie über p und q. Dann gilt:
Die Summe der gegenüberliegenden Flächen ist gleich der Summe der anderen 2 gebenüberliegenden Flächen.
Zu diesem Satz kommt man über den Höhensatz des Euklid:
h²=a²-q²
h²= b²-p²
Wenn man die beiden rechten Seiten gleichsetzt, ergibt sich:
a²-q² = b²-p²
Umgestellt ergibt sich:
a²+p² = b²+q² qed
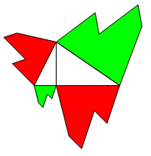
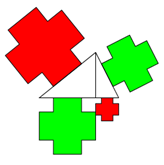
Aufgabe: Programmieren Sie in Geogebra oder einem ähnlichen Programm ein durch Schieberegler frei wählbares
rechtwinkliges 3-Eck, auf dessen Hypotenuse das Lot gefällt wird. Stellen Sie verschiedene Figuren über die Seiten!
|
|
7.6 |
Pythagoras: Flächengleichheit bei 1 rechtwinkligen 3-Eck und Ketten von Figuren
Normalerweise wird je 1 Figur an jede Seite eines rechtwinkligen 3-Ecks gehängt.
Welche Gesetzmäßigkeiten gelten, wenn stattdessen ganze Ketten von Figuren an jede Seite des rechtwinkligen 3-Ecks gehängt werden?
Wenn die Kettenfiguren auf allen 3 Seiten nach den gleichen Regeln angesetzt werden, dann gilt:
Theorem 1: Für jedes Kettenglied gilt ka²+kb²=kc²
Theorem 2: Für alle Kettenglieder der 3 Arme in Summe gilt: ka²+kb²=kc²
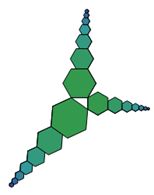
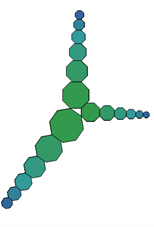
Zu geringelten Armen kommt man bei regelmäßigen Vielecken mit ungerader Anzahl von Ecken.
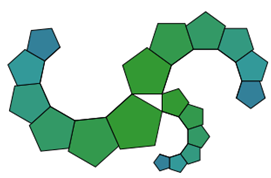
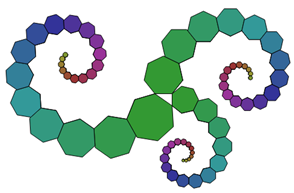
Aufgabe: Setzen Sie die Ketten an anderen Seiten des Vielecks an, um Überschneidungen zu vermeiden!
|
|
7.7 |
Pythagoras-Mund
Bei einem Pythagoras-Mund findet man Ketten von rechtwinkligen 3-Ecken. Dabei gilt: Die Flächen von 2 benachbarten schwarzen
Feldern sind gleich der Fläche des dazugehörigen roten Feldes.


|
|
7.8 |
Pythagoras: Flächenverhältnisse bei einem 3-Eck mit eingeschriebenen Quadraten
Bei Wolfram Mathworld findet man ein right triangle, in das Quadrate so eingeschrieben werden, dass sie abwechselnd
an der einen Kathete und der Hypotenuse kleben.
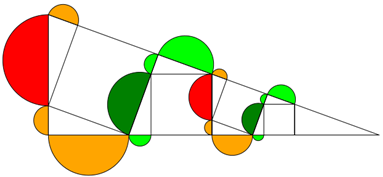
Hier gilt: Die Fläche eines großen Halbkreises ist gleich der Fläche der dazugehörigen 3 Halbkreise zu beiden Seiten.
Das versteht man schnell, wenn man eine Quadrat-Seite mit 2 Halbkreisen um 90° dreht.
Aufgabe: Welche Flächensätze finden Sie heraus?
|
|
8 |
Quellen
http://aghandoura.com/DINAMIC/T11FINAL/T11/7/7.htm :5-Eck
http://aghandoura.com/DINAMIC/T11FINAL/T11/8/8.htm :6-Eck
http://aghandoura.com/DINAMIC/T11FINAL/T11/9/9.htm :8-Eck
http://did.mat.uni-bayreuth.de/geonet/beispiele/pdf/pythagoras.pdf :Zufallsfigur, Bilder von Pythagoras, Halbkreise
http://elmaestrodecasas.blogspot.com/2011/08/matematicas-para-albaniles-mas-sobre-el.html :3-Ecke, 6-Ecke, Halbkreise
http://geometrie.zum.de/wiki/Der_Satz_des_Pythagoras_-_Eine_didaktische_Umsetzung :Dreiecke
http://ggbconference2009.pbworks.com/f/Stelling+van+Pythagoras.pdf :3-Eck, Halbkreis, Trapez, Gebirge, gemischte Figuren
http://gogeometry.com/pythagoras/right_triangle_formulas_facts.htm :Puzzle-Teil
http://images.math.cnrs.fr/Encore-une-preuve-du-theoreme-de-Pythagore.html?lang=fr :3-Eck, 5-Eck, Nilpferde
http://jwilson.coe.uga.edu/EMAT6680Fa2012/Smith/6690/pythagorean%20theorem/KLS_Pythagorean_Theorem.html :Pythagorean Theorem, by Kassie Smith, Halbkreise, Dreiecke, Rechtecke, 5-Ecke, 6-Ecke, Figures composed of two shapes above, Random Figures
http://mathspace.pl/matematyka/uogolnione-twierdzenie-pitagorasa/ :Halbkreis
http://tinspire-education.blogspot.com/2013/06/blog-post_1559.html :3-Eck, Halbkreis
http://utenti.quipo.it/base5/pitagora/tritagora.htm :3-Eck mit Zerlegung in Quadrat, Dreiecksbaum, Umwandlung von Pythagoras-Quadraten in andere Formen
http://www.boelte.homepage.t-online.de/seiten/verallgemeinerung.html :Haus mit Dach symmetrisch zur Senkrechten
http://www.edugains.ca/resourcesMath/CE/LessonsSupports/TIPS4RM/Grade8English/Unit10_VisualizingGeometricRelationships.pdf :6-Eck, Halbkreis
http://www.fisem.org/www/union/revistas/2018/54/05.pdf :Beweis zu unregelmäßigen 8-Ecken (Treppen), Beweis zu gleichschenkligen Trapezen, Beweis zu gleichseitigen Dreiecken, Halbkreis, Halbkreis+halbes Quadrat, 3-Eck, 5-Eck, 6-Eck
http://www.fisem.org/www/union/revistas/2018/54/05.pdf :Halbkreise, Halbkreise plus Rechtecke, 3-Ecke, 5-Ecke, 6-Ecke
http://www.grupoalquerque.es/ferias/2007/generalizarpitagoras/generapitagoras.htm :3-Ecke, Parallelogramme, 6-Ecke, Trapeze - jeweils mit Zerlegungsbeweisen
http://www.mathpoint.ch/12planimetrie/pythagoras.html :Rechtwinklige 3-Ecke, Fläche unter Kurve
http://www.philmath.org/Pythagoras.pdf :gleichschenklige Dreiecke
http://zibalsc.blogspot.com/2013/05/122-teorema-di-pitagora.html :5-Sterne, 3-Eck, 5-Eck
https://areeweb.polito.it/didattica/polymath/htmlS/argoment/APPUNTI/TESTI/Gen_02/Cap7.html :5-Eck, Halbkreis
https://articuweb.wordpress.com/2010/05/15/teorema-de-pitagoras-y-demostracion/ :8-Ecke, 5-Ecke, 6-Ecke, Halbkreise, Gebilde mit 4 Zacken, unregelmäßiges Tierbild
https://artofproblemsolving.com/wiki/index.php/2002_AMC_8_Problems/Problem_16 :rechtwinkl. 3-Eck
https://bajdocja.blogspot.com/2019/04/wielkanocna-wersja-twierdzenia.html :Halbkreis
https://betterlesson.com/lesson/590441/reviewing-the-pythagorean-theorem :Ente
https://blogdemaths.wordpress.com/2017/08/13/pythagore-sous-toutes-ses-formes-geometriques/ :gleichseitige Dreiecke, Sechsecke, Halbkreise, Bild von Pythagoras, gefüllte Kochkurvenfigur, Phantasieform
https://christianrohrbach.net/wp-content/uploads/45-Satz-des-Pythagoras.pdf :5-Sterne, Halbkreise, Bild von Pythagoras
https://clubdematematicasnewton.blogspot.com/2014/07/generalizacion-del-teorema-de-pitagoras.html :5-Ecke, 3-Ecke, Halbkreise, unregelmäßige Flächen wie Kurve
https://danpearcymaths.wordpress.com/2012/05/09/do-we-need-the-pythagoras-theorem/ :Bild der Mona Lisa
https://danpearcymaths.wordpress.com/2012/05/09/do-we-need-the-pythagoras-theorem/ :Mona Lisa
https://de.wikipedia.org/wiki/Satz_des_Pythagoras :regelmäßige Fünfecke, Dreiecke, ganze Kreise
https://debart.pagesperso-orange.fr/geoplan/pythagore.mobile.html :Halbkreise
https://demonstrations.wolfram.com/AnotherGeneralizationOfPythagorassTheorem/ :Parallelogramm
https://demonstrations.wolfram.com/GeneralizedPythagorasTheorem/ :unregelmäßige 3-Ecke, 4-Ecke, bizarres Gebilde wie ein Kopf mit Auge
https://demonstrations.wolfram.com/PythagoreanTheoremForRegularPolygons/ :3-Ecke bis 8-Ecke mit unterschiedlichen Dreiecks-Winkeln
https://docplayer.it/13414788-Teorema-di-pitagora-scuola-italica.html :5-Eck, Halbkreis, Vielecke in einem Bild
https://documen.site/download/il-giardino-di-archimede_pdf :Phantasie-Figur, 6-Eck
https://en.wikipedia.org/wiki/Pythagorean_theorem :regelmäßige Fünfecke, rechtwinklige Dreiecke, unregelmäßige Dreiecke
https://fachportal.lernnetz.de/files/Inhalte%20der%20Unterrichtsf%C3%A4cher/Mathematik/oberste%20Ebene/Unterrichtsmaterialien/zu%20den%20Fachanforderungen%20Sek.%20I/zum%20Leitfaden%20Sek.%20I/2.%20Anforderungsebenen%20und%20-bereiche/Aufgabenbeispiele_zum_erwarteten_Output_der_Unterrichtseinheit_Pythagoras_%28pdf%29.pdf :Halbkreise
https://fr.wikipedia.org/wiki/Fichier:PythagoreEuclide1.gif :Beweise zu diagonal zu Dreiecken halbierten Quadraten
https://geometriapdf.blogspot.com/2018/07/areas-circulares-teoria-y-formulas-de.html :Halbkreis, 3-Eck
https://ichi.pro/de/ein-wirklich-eleganter-beweis-224499681350610 :unregelmäßige Dreiecke, Zufallsform
https://infourok.ru/prezentaciya-po-geometrii-klass-teorema-pifagora-340981.html :Halbkreis, Möndchen, abgeschnittener Halbkreis
https://kopilkaurokov.ru/matematika/uroki/mietodichieskaia-razrabotka-uroka-po-tiemie-tieoriema-pifaghora :Halbkreis
https://learnattack.de/schuelerlexikon/mathematik/verallgemeinerter-satz-des-pythagoras :Halbkreise, nicht-symmetrisches Gebäude
https://library.weschool.com/lezione/pitagora-teorema-formule-dimostrazione-geometria-piana-12700.html :unregelmäßiges 3-Eck
https://liyuansuarez.jimdofree.com/2013/09/05/los-otros-teoremas-de-pitagoras/ :Kreis, gleichseitiges 3-Eck, 5-Stern, 8-Stern, 6-Eck
https://marcelomendizabal.wordpress.com/2017/02/06/se-puede-generalizar-el-teorema-de-pitagoras/ :5-Eck, 6-Eck, 8-Eck, Halbkreis
https://mathothek.de/katalog/der-satz-des-pythagoras-der-wohl-bekannteste-satz-der-mathematik/ :Halbkreise
https://mathspace.pl/matematyka/uogolnione-twierdzenie-pitagorasa/ :Halbkreis
https://moluch.ru/conf/ped/archive/22/1991/ :Bild von Mann mit Perücke. 3-Eck, 6-Eck, Halbkreis
https://momath.org/home/pythagorean-crackers/ :gleichseitige Dreiecke, Phantasie-Gebilde (Damenschuhe?)
https://php.math.unifi.it/archimede/archimede/pitagora/exh_pitagora/schede.php?id=6 :5-Sterne, Halbkreis
https://poetrywithmathematics.blogspot.com/2015/12/generalized-pythagorean-theorem-visual.html :3-Eck bis 9-Eck, Viertelkreis
https://portalacademico.cch.unam.mx/matematicas2/teorema-pitagoras/semicirculos :Halbkreis
https://ppt-online.org/541111 :Halbkreis, Möndchen, abgeschnittener Halbkreis
https://regolo54.tumblr.com/post/149691623447/geometry :3-Eck bis 6-Eck in einer Figur
https://revistas.unc.edu.ar/index.php/REM/article/view/10207 :Halbkreis, Doppel-Quadrat, 3-Eck, 6-Eck, 5-Eck konkav, Phantasie-Gebilde
https://scask.ru/a_book_e_math.php?id=103 :Halbkreis
https://soymatematicas.com/teorema-de-pitagoras/ :3-Ecke, 5-Ecke, Bild von Nilpferd
https://stringfixer.com/ar/Pythagorean_theorem :3-Eck, 5-Eck
https://teoremadepitagoras.info/teorema-de-pitagoras-formula/ : Halbkreise
https://thecognitivecondition.com/?p=168 :Steve Wait, 2 unregelmäßige Vierecke und ihre Zusammenfügung, 2 quadrilaterals
https://toolbox.edu.tum.de/visualisierungen/modul01/Applets/ZerlegungsgleichN-Eck.html :3-Eck, 5-Eck, 6-Eck, 7-Eck, Zerlegungsbeweis
https://twitter.com/longformmath/status/1275462160588500992?lang=de :Halbkreis, Bild von Homer Simpson
https://uzumakirey21.weebly.com/ :3-Eck
https://www.archimedes-lab.org/atelier.html?https://www.archimedes-lab.org/pzm4b.html :3-Ecke, 6-Ecke, Zerlegungen
https://www.br.de/mediathek/video/mathematik-zum-anfassen-der-satz-des-pythagoras-av:5d138dd0b0c881001ae02a21 :Kaninchen, 5-Sterne
https://www.buscalibre.us/libro-teorema-de-pitagoras-madera-27x38-cms-caja-con-tapa-6-puzzles-formas-geometricas/4536704/p/4536704 :3-Eck, Halbkreis
https://www.chegg.com/homework-help/questions-and-answers/suppose-know-pythagorean-theorems-states-sum-areas-squares-built-upon-two-legs-right-trian-q56686910 :3-Eck, Rechteck, 5-Eck, 6-Eck, Halbkreis, Halbkreis+Dreieck
https://www.cut-the-knot.org/pythagoras/index.shtml :Halbkreis, konkaves 4-Eck
https://www.ecured.cu/Teorema_de_Pit%C3%A1goras :Halbkreis
https://www.eoswetenschap.eu/pythagoras :3-Eck, 5-Eck, Halbkreis
https://www.festascienzafilosofia.it/2017/03/dimostrazione-dellenunciato-del-teorema-di-pitagora-con-poligoni-regolari-costruii-sui-lati-o-semicirconferenze-aventi-come-diametro-i-lati/ :6-Eck
https://www.festascienzafilosofia.it/2017/03/teorema-di-pitagora-12/ :6-Eck
https://www.festascienzafilosofia.it/2017/03/teorema-di-pitagora-3/ : 6-Eck, Halbkreis
https://www.festascienzafilosofia.it/2017/03/teorema-di-pitagora-6/ :Vielecke in einem Bild, unregelmäßiges 3-Eck
https://www.festascienzafilosofia.it/page/61/?sentence=paper-first-introduction-the-sentence-research-of-constitution.phtml :gleichschenkliges 3-Eck, Halbkreis, 6-Eck, Vielecke, gleichseitiges 3-Eck
https://www.geogebra.org/m/dbbbjmhm :Steve Phelps 3-Eck Zerlegungsbeweis
https://www.geogebra.org/m/eWDynsQG :3- Eck bis 9-Eck
https://www.geogebra.org/m/exrpd9dw :Steve Phelps 6-Eck Zerlegungsbeweis
https://www.geogebra.org/m/gCKmvS4S :Vielecke
https://www.geogebra.org/m/gmdjhr4k :Beweis zu regelmäßigem 5-Eck
https://www.geogebra.org/m/gVbHQdtV :Halbkreis
https://www.geogebra.org/m/j8FRw7E7 :3-Ecke, Halbkreise
https://www.geogebra.org/m/KYcxAm9m :5-Ecke
https://www.geogebra.org/m/q5knv6bw :Steve Phelps 3-Ecke bis 8-Ecke Zerlegungsbeweis Geogebra
https://www.geogebra.org/m/u3jwj2sa :Steve Phelps 5-Eck Zerlegungsbeweis
https://www.geogebra.org/m/vtDjfM6g :n-Ecke
https://www.geogebra.org/m/Whp8WMrb :Pythagoras-Figur
https://www.geogebra.org/m/y2QMXs8m :n-Ecke
https://www.geogebra.org/m/y65sue7u :Steve Phelps 3-Eck Zerlegungsbeweis
https://www.geogebra.org/m/YaYPDzSJ :3-Ecke Zerlegungsbeweis
https://www.geogebra.org/m/ZQU4paJV :Vielecke Geogebra
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjEqOzX5OfwAhWLgv0HHXbPD7IQFjABegQIBBAD&url=https%3A%2F%2Frevistas.unc.edu.ar%2Findex.php%2FREM%2Farticle%2Fdownload%2F10207%2F10857%2F26958&usg=AOvVaw05IppmHmziy0MMVm0u-4_5 :Halbkreis, Doppel-Quadrat, 3-Eck, 6-Eck verzerrt, 5-Eck konkav, Phantasiegebilde
https://www.icportotolle.edu.it/sites/default/files/copy-of-old-site/Sito_Porto_Tolle/www.icportotolle.gov.it/geogebra9b5f.html?start=5 :Vielecke, Geogebra
https://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/satz-des-pythagoras :Halbkreise, unsymmetrische Dreiecke
https://www.maa.org/press/periodicals/convergence/pythagorean-cuts-extensions-to-regular-polygons :6-Eck
https://www.matematicasonline.es/terceroeso/apuntes/problemas-metricos.pdf :Dreieck, Halbkreis
https://www.math.uni-bielefeld.de/~ringel/puzzle/puzzle02/pytha-na.htm :Halbkreis, 6-Eck, Kringel
https://www.mathematik-nachhilfe.de/wp-content/uploads/Pythagoras.pdf :3-Eck, 5-Eck, Halbkreis
https://www.medianauka.pl/twierdzenie-Pitagorasa :Bilder von Telefonen
https://www.pasqualeclarizio.it/il-teorema-di-pitagora-puo-essere-dimostrato/ :5-Eck
https://www.pinterest.com.au/pin/633387428035632/ :Kreise
https://www.pinterest.de/pin/155726099588791857/ :5-Sterne
https://www.pngwing.com/ru/free-png-mqpat :Halbkreis
https://www.redbubble.com/de/i/metallbild/Euklids-Elemente-Buch-1-Prop-47-GeoBunies-von-2redheadedbros/13077351.0JXQP :Comic-Bilder von Kaninchen
https://www.redusoft.de/info/mathprof-hilfe/verallgemeinerung-des-satz-des-pythagoras.html :Saugglockenform, Zufallsform, halbes Zwölfeck, Kreisteil
https://www.saatchiart.com/art/Painting-THE-PYTHAGOREAN-THEOREM-Alternative-Version/26236/3997356/view :"THE PYTHAGOREAN THEOREM (Alternative Version)," by Ronis Varlaam, Kreise
https://www.shapeways.com/product/2GVQTW6X7/the-triangles-of-pythagoras-puzzle :3-Ecke
https://www.shapeways.com/product/2GVQTW6X7/the-triangles-of-pythagoras-puzzle :3-Ecke
https://www.thinglink.com/scene/637971318389604354 :5-Sterne
https://www.transum.org/Software/Fun_Maths/Trivia.asp :5-Eck
https://www.uibk.ac.at/mathematik/algebra/media/teaching/diplomarbeit_sara-tirler.pdf :Kopie der Abbildung von Strick (siehe unten)
https://www.uv.es/lonjedo/esoProblemas/3eso14triangulo.pdf :3-Ecke, 6-Ecke, Halbkreise
https://www.walser-h-m.ch/hans/Miniaturen/E/Epstein-Nielsen/Epstein-Nielsen.htm :rechtwinklige gleichschenklige Dreiecke, halbe Quadrate in Form von Trapezen; Zerlegungsbeweise
https://www.walser-h-m.ch/hans/Miniaturen/M/Moendchen2/Moendchen2.htm :Möndchen
https://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_m_rw_Dreiecken/Pyth_m_rw_Dreiecken.htm :Bild von Pythagoras, rechtwinklige Dreiecke
https://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_m_Vielecken/Pyth_m_Vielecken.htm :regelmäßige Vielecke (3- bis 8-Ecke)
https://www.walser-h-m.ch/hans/Miniaturen/P/Pythagoras_und_kein_Ende/Pythagoras_und_kein_Ende.pdf :Halbkreis, 3-Eck, Pythagoras-Schnecke Halbkreise, 3-Ecke, gleichschenklige 3-Ecke, 5-Ecke, Pythagoras-Straße Halbkreise, Quadrat aus gleichschenkligen 3-Ecken
https://www.walser-h-m.ch/hans/Vortraege/20160204/Puzzle.htm :Beweise zu 3-Ecken, 5-Ecken, 6-Ecken, 7-Ecken, 8-Ecken, alternative Teilungsbeweise für 3-Ecke
https://www.walser-h-m.ch/hans/Vortraege/Vortrag97/Puzzle.pdf :5-Eck
https://www.wikiwand.com/ru/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%B0 :3-Eck, rechtwinklige 3-Ecke
https://www.youtube.com/watch?v=_PvXQe4yatc :Halbkreis, 3-Eck, 5-Eck, 6-Eck, 7-Eck, 8-Eck
https://www.youtube.com/watch?v=5hJAqtZPDSE :3-Eck, 5-Eck, 7-Eck
https://www.youtube.com/watch?v=6rCdvPI40R4 :6-Ecke, verzerrt, Halbkreise
https://www.youtube.com/watch?v=6zavr1NVuyA :3 - 10-Ecke
https://www.youtube.com/watch?v=86sep144gq8 :gedrehte Quadrate
https://www.youtube.com/watch?v=94qhP1FItV4 :Beweis zu gleichseitigen Dreiecken
https://www.youtube.com/watch?v=bRWAYNDOtgY :Generalizzazione del teorema di Pitagora; 3 – 19-Eck
https://www.youtube.com/watch?v=ci8YhZtyeX8 :3 – 8-Eck, Halbkreis
https://www.youtube.com/watch?v=dMdLnrZgZRI :3 – 12-Ecke
https://www.youtube.com/watch?v=Fc107DDENfo :3-Eck
https://www.youtube.com/watch?v=Flf781eTaJQ :Halbkreis, 3-Eck
https://www.youtube.com/watch?v=Ir3MUW_VkgQ :Halbkreis
https://www.youtube.com/watch?v=JHh9mwI_X9s :3-Eck, 5-Eck
https://www.youtube.com/watch?v=K6FWZNtQWkA :3-Eck, 5-Eck, 8-Eck, 10-Eck, unregelmäßiges 4-Eck, Halbkreis
https://www.youtube.com/watch?v=KNjkXWK7ukE :6-Eck, Halbkreis
https://www.youtube.com/watch?v=p-0SOWbzUYI :Halbkreis, 5-Eck, Bild eines Gesichts
https://www.youtube.com/watch?v=PhDzOlGkU20 :3-Eck
https://www.youtube.com/watch?v=Pvx1fP__YA8 :5-Eck
https://www.youtube.com/watch?v=qUGttT47e_s :5-Eck, 6-Eck, 7-Eck
https://www.youtube.com/watch?v=UWb1gX_BE_4 :3-Eck, Halbkreis, 5-Eck, 6-Eck
https://www.youtube.com/watch?v=WTQ71IjVnoE :3-Eck, 5-Eck
https://www.youtube.com/watch?v=XhUkmv-oLTA :3 – 8-Eck
https://www.youtube.com/watch?v=Y0IKzZgrWZk :Teorema di Pitagora generalizzato; 5 - 8-Eck z.B. Halbkreis-Folgen, Dreiecks-Folgen, 5-Ecks-Folgen
https://www.youtube.com/watch?v=YG8u1g2r8os :3-Eck, Halbkreis, 5-Eck, 6-Eck
H.E.Dudeney, Amusements in Mathematics, Puzzle No. 148, Halbkreise
Zeitschrift "Mathematik lehren" Nr. 216, Cover zu "Pythagoras vielfältig erleben", Bild (Weber/Musiker?) maßstabsgetreu vergrößert
Heinz Klaus Strick, Mathematik ist schön, 2. Aufl. S. 352, Dreieck bis Sechseck, Achteck, Halbkreise
Ivan Moscovich, Formenrätsel, Fleurus Idee Verlag 2005, S. 50, Dreieck bis Sechseck, Viertelkreis
Ivan Moscovich, The Puzzle Universe: A History of Mathematics in 315 Puzzles, Firefly Books, 2015
JULIO CESAR BARRETO GARCÍA, Teorema de Pitagoras: Un estudio del metodo geometrico al calculo integral con aplicaciones (Coleccion de Secundaria, Band 4) 2014: Dreiecke, kurvilineare Figuren
Heinrich Hemme, Die Sphinx, Göttingen 1994, Aufgabe Nr. 45, "Der Satz des Pythagoras" - gleichseitige Dreiecke, Halbkreise
|
|
|















































































































