Dreiecke mit flexiblem Innendreieck

Homepage von Volker Pöhls

Dreiecke mit flexiblem Innendreieck Antwort auf Hans Walsers Seite "Dreieck dritteln"
1
Worum geht es? Der Schweizer Mathematiker Hans Walser hat eine seiner Seiten mit mathematischen "Miniaturen" dem Thema Dreieck dritteln gewidmet. Die Seite ist 2012 entstanden und 2020 erweitert worden. Normalerweise wird das Wort "dritteln" in der Bedeutung "in drei gleiche Teile teilen" verwendet (Duden, wiktionary). Hans Walser hat eine andere Bedeutung im Sinn: Dritteln = eine zusammenhängende Fläche abteilen, die ein Drittel der Ausgangsfläche bedeckt. Es gibt zahlreiche Möglichkeiten, eine Drittelfläche eines Dreiecks zu isolieren: 3 kongruente Teilflächen 3 nicht-kongruente Teilflächen 1 Fläche mit einer Fläche von einem Drittel Es gibt wiederum zahlreiche Möglichkeiten, eine Fläche von einem Drittel in einem Dreieck zu bestimmen. Walser hat sich eine bestimmte davon ausgesucht. 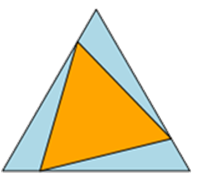Seine Fragestellung scheint zu sein: Wie kann man ein Dreieck so in ein Dreieck einpassen, dass alle drei Ecken eine andere Seite des Ausgangsdreiecks berühren und die Fläche ein Drittel der Gesamtfläche beträgt? Seine Antwort lautet, dass man dies erreicht, indem man die Seiten des Ausgangsdreiecks drittelt und jeweils den ersten Punkt mit dem ersten Punkt der nächsten Seite verbindet. 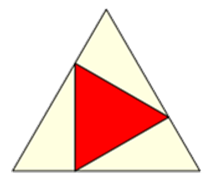. Walser beweist diese Behauptung mittels einer Zerlegung in 18 kongruente Teile. Durch Einfärbung mit 6 verschiedenen Farben zeigt er: "Jedes Puzzleteil kommt einmal innen und zweimal außen vor." Da das Verhältnis innen zu außen also 1 : 2 beträgt, muss die Innenfläche 1/3 betragen.
2
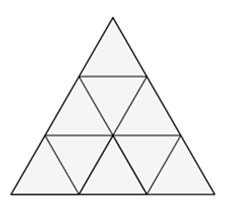
Alternativer Beweis Ein Dreieck lässt sich einfach in 9 gleiche Teile zerlegen. Auf diese Weite hat man also eine Neuntelung des Dreiecks erzeugt. Die Fläche eines Dreiecks berechnet sich über Grundseite * Höhe * 0,5. Wenn man die beiden mittleren Punkte einer Seite mit dem ersten Punkt der Nachbarseite verbindet, hat man ein neues Dreieck der Fläche 1/9 erzeugt. Zusammen mit dem kleinen Dreieck rechts unten ergibt das eine Fläche von 2/9. Wenn man eine solche Abteilung an allen 3 Ecken wiederholt, so hat man in den 3 Ecken eine Fläche von 3 * 2/9 = 6/9 = 2/3 erzeugt. Daraus folgt, dass der Rest, nämlich das Dreieck in der Mitte, eine Fläche von 1/3 haben muss. 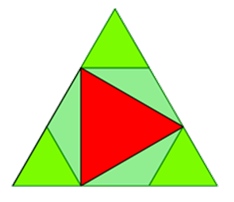Das Interessante an dieser Art von Beweis ist, dass er ohne Färbung auskommt (hier nur zur Verdeutlichung, von welchen Dreiecken die Rede ist), das Ausgangsdreieck nur in 7 Teile zerlegt wird und die Fläche innen durch einfache Differenzbildung berechnet wird. Die Viertelung eins Dreiecks ist - wie die Neuntelung (siehe oben) - relativ trivial. 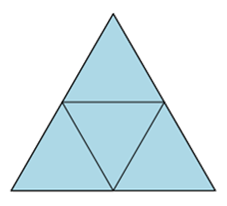Nicht so trival ist dagegen die Halbierung (oder 2/3ung oder 90%isierung) eines Dreiecks, so dass in der Mitte ein Dreieck entsteht, dessen Ecken wie beim Walser-Dreieck auf den Seiten des Ausgangsdreiecks liegen.
3
Dreiecke mit flexiblem Innendreieck In der Walser-Aufgabe befanden sich die Ecken des neuen Dreiecks jeweils bei 1/3 (bzw. 2/3) der Seite, bei der Viertelung bei 1/2 der Seite. Kann man Innendreiecke auch erzeugen, indem man andere Faktoren als 1/2, 1/3 oder 2/3 nimmt? Wie berechnet sich dann die Fläche des Innendreiecks? Umgekehrt: Bei gegebenem Anteil der Innenfläche, wie berechnet man den Seitenfaktor? 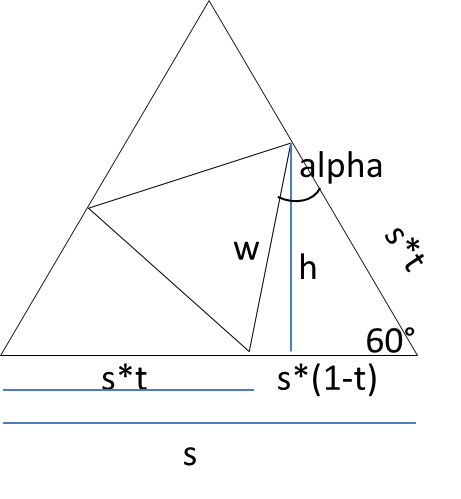Gehen wir zunächst der Einfachkeit halber von einem gleichseitigen Dreieck aus (und hoffen, dass sich die Überlegungen - wie bei Walser - auf ein beliebiges Dreieck übertragen lassen.) Die Höhe in einem gleichseitigen Dreieck muss man nicht selbst ausrechnen; man findet sie in einer Formelsammlung oder im Internet: (sqrt 3)/2s. Fläche des gleichseitigen Ausgangsdreiecks: Grundseite Höhe * 0,5 = s(sqrt 3)/2s0,5 = (sqrt 3)/4s^2 Nennen wir den Teilungs-Faktor t (der bei Walser 1/3 beträgt). Die Höhe h liegt an einem rechtwinkligen Dreieck; sie lässt sich also wie folgt berechnen: Gegenkathete = Hypotenusesin 60° sin 60° = (sqrt 3)/2 h = st(sqrt 3)/2 Jetzt lässt sich die Fläche eines Außendreiecks berechnen: Grundseite Höhe * 0,5 = (1-t)sst(sqrt 3)/20,5 = (1-t)t* (sqrt 3)/4s^2 Da es 3 Außendreiecke sind, beträgt ihre Gesamtfläche: 3(1-t)t (sqrt 3)/4s^2 Der Anteil der Innenfläche an der Gesamtfläche beträgt also: (sqrt 3)/4s^2- 3(1-t)t* (sqrt 3)/4s^2 / (sqrt 3)/4s^2 Durch Kürzen erhält man: *FAnt= 1- 3t(1-t)** Um den Teilungsfaktor bei gegebenem Flächenanteil zu berechnen, muss man diese Gleichung nach t auflösen: FAnt= 1- 3t(1-t) 0 = 3t² - 3t +1 - FAnt 0 = t² - t - (FAnt-1)/3 t = 0,5 +- sqrt(1/4+(FAnt-1)/3)* Wenn Sie Lust haben, berechnen Sie anhand dieser 2 Formeln: Zur Probe den Flächenanteil des Innendreiecks bei einem Faktor t= 0,5 t=1/3 Neue Aufgaben: t=0,4 t=0,175 Zur Probe den Seitenfaktor t bei einem Flächenanteil von FAnt= 1/4 FAnt= 1/3 FAnt= 1/2 FAnt= 2/3 FAnt= 90% Um das Ergebnisdreieck z.B. über jsLOGO programmiert zeichnen zu können, braucht man noch den Winkel alpha und die Seitenlänge des Innendreiecks. Im Außendreieck sind 2 Seiten und ein Winkel bekannt. Die Seitenlänge w des Innendreiecks lässt sich deshalb über den Kosinussatz berechnen. Der Winkel alpha lässt sich dann über den Kosinussatz oder den Sinussatz berechnen. Jetzt kann man das Dreieck so programmieren, dass der Seitenfaktor t als variabler Parameter eingegeben werden kann.
4
Parkettierungen mit Dreieck im Dreieck Bleiben wir erst einmal (wie bei Hans Walser) bei einem Dreieck, in das ein Dreieck nach einer Strecke von 1/3 Grundseite eingeschrieben wird. Es gibt einige alternative Parkettierungen. Zunächst könnte man sich auf eine einzige "Kachel" beschränken. Etwas lebhafter wird es, wenn man 2 verschiedene Kacheln nimmt, nämlich die, auf der die Innendreiecke nach 1/3 und 2/3 Grundseite konstruiert werden. 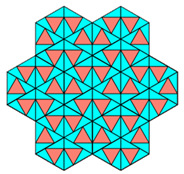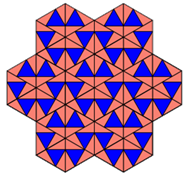Jetzt hat man zunächst die raffinierte Parkettierung von Walser, bei der alle Innendreiecke an den Spitzen miteinander verbunden sind: Aber es gibt noch andere symmetrische tesselations ("Pfeil", "Blatt", "Amboss"): Und man kann die Dreiecke ja auch nach Zufallssystem auf der Ebene platzieren. 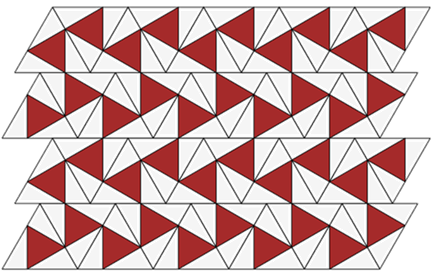Die Startdreiecke können auch zueinander verschoben werden: Welche Varianten fallen Ihnen ein ? Da in den Ausgangsdreiecken das Flächen-Verhältnis 1:2 ist und die großen Parkette nur aus vollständigen Ausgangsdreiecken bestehen, ist das Flächen-Verhältnis des Gesamt-Parketts ebenfalls 1:2.
5
Parkettierungen mit Dreiecken mit flexiblem Innendreieck Noch abwechslungsreicher wird es, wenn man die Dreiecke mit Innendreiecken mit flexibler Teilkante auf der Fläche verteilt. Es gibt unendlich viele Kombinationsmöglichkeiten. Welche Varianten fallen Ihnen ein ?
6
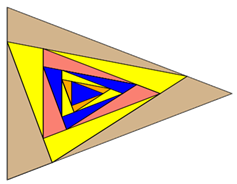
Form der Innendreiecke bei Iteration Hans Walser stellt fest, dass bei verzerrten 1/3 Dreiecken die Form des ersten Innendreiecks anders ist, während sie beim zweiten Innendreieck wiederkehrt. Das ist bei Dreiecken mit anderem Seitenfaktor anders. Wenn Seiten und Winkel des Innendreiecks berechenbar sind, dann müssten auch Seiten und Winkel von iterativ erzeugten Innendreiecken berechenbar sein. Ergo müsste man berechnen können, wann Innendreiecke dem Startdreieck ähnlich sind. Wenn man jedoch für das zweite Innendreieck den komplementären Seitenfaktor einsetzt, scheint die alte Form wieder zurückzukehren.
7
Diverses 1.) Gelten die obigen Überlegungen nicht nur für gleichseitige, sondern beliebige Dreiecke (vgl. Hans Walsers Beweisführungen)? 2.) Gibt es (außer bei den Seitenfaktoren 1/3, 1/2 und 2/3) weitere Fälle, bei denen Flächenanteil und Seitenfaktor rel. "glatte" Werte annehmen? 3.) Wie lassen sich Animationen von Dreiecken mit gleitenden Seitenfaktoren von 0 bis 1 erstellen? Geht es vielleicht mit GEOGEBRA? 4.) Bei welchem t erhält man ein Innendreieck mit 2/3 der Gesamtfläche? Eingesetzt in die t-Formel: t= ½ - sqrt(5)/6 Wenn die Hälfte aller Innen-Dreiecke 1/3 der Dreiecksfläche haben, die andere Hälfte aller Innen-Dreiecke 2/3 der Dreiecksfläche, dann hat die Gesamtfläche eine Verteilung von 1:1. 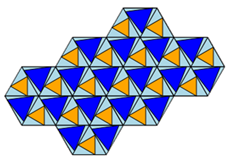5.) Ähnliches Thema für eine neue Miniatur: Welches Flächenverhältnis ergibt sich, wenn man ein Dreieck an den 3 Ecken kupiert um gleichschenklige Dreiecke mit der Grundseite t*große Grundseite?