|
Do it yourself: Bunte geometrische Objekte mit JSLogo |
|
|
Im Netz stehen unzählige geometrische Bilder zur Verfügung. Das Besondere an dieser Seite ist, dass sie nicht nur
hübsche bunte Bilder zeigt, sondern den User in die Lage versetzt, diese Bilder selbst herzustellen.
Es geht also um das Selbermachen, zumindest das Nachmachen und Variieren. Das bedeutet auch, dass man danach
auf seine Ergebnisse stolz sein kann - wie ein Handwerker nach vollbrachter Leistung.
Logo ist eine Programmiersprache, die für Programmier-Laien geeignet ist, weil sie vergleichsweise einfach
und anschaulich ist.
Typisch für LOGO ist die virtuelle Schildkröte (engl. Turtle), die der Programmierer mit eckigen Bewegungen über den
Bildschirm laufen lässt, wobei sie eine Linie hinter sich herzieht. Auf diese Art können die tollsten Zeichnungen erstellt werden.
Logo gibt es in vielen Dialekten. Die Vorteile des Dialekts JSLogo für den User, also für SIE, sind folgende:
- kostenlos
- keine Anmeldung, keine Registrierung
- kein Herunterladen von Dateien
- relativ einfach zu lernen, auch für Kinder
- Auch ohne die geringsten Kenntnisse kann man tolle Objekte auf den Bildschirm zaubern.
- Automatisch werden alle selbst gebauten Programme gespeichert.
Dem User steht das Programm jederzeit im Nullkommanix online fix und fertig zur Verfügung.
Nachteile gibt es natürlich auch. So basiert JSLogo auf Englisch, ohne Arbeit und Lernen kann man best.
gewünschte Ergebnisse nicht erzeugen,
das Programm hat seine Grenzen, die Farb-Möglichkeiten sind begrenzt, aus anderen Dialekten muss erst in den JSLogo-Dialekt übersetzt werden bzw. umgekehrt, usw.
Also nichts wie ran!
|
So sieht die Startseite von JSLogo aus
|
Wie gehen Sie vor?
Sie möchten in 2 Minuten ein tolles Bild erzeugen? Wie geht das?
- JSLogo öffnen
- Einen Programmcode (z.B. einen Code weiter unten auf dieser Seite) durch copy und paste (kopieren und einfügen) in das Feld links unten einfügen.
- Das Programm laufen lassen, indem man auf den Knopf "Run" unten in der Mitte drückt
- Das Ergebnis entsteht im Ergebnisfenster oben links.
- Das Ergebnis bei Bedarf speichern oder in die Zwischenablage kopieren und seinen Freunden schicken.
Wie? Über den Punkt EXTRAS auf der rechten Bildschirmseite, dann DOWNLOAD DRAWING, ÖFFNEN MIT und OKAY
Sie öffnen JSLogo in einem neuen Fenster, also auf einer zweiten Seite.
Das geht am einfachsten, indem Sie auf diesen Link zu JSLogo klicken.
Das Ergebnis ist ein Bildschirm, der wie auf dem Bild in der Mitte aussieht. Links ist das Ergebnis-Fenster, unten das
Fenster für den Programm-Code, rechts findet man allerlei Nützliches wie den Befehlsvorrat, Links etc.
|
|
Beispiel 1 - Kreiselkreise: Programm-Code
to kreis.boegen :r :anz :dir
; h=:r/2*3
; h^2+s^2/4=s^2
make "h :r/2*3
make "s 2*:h*sqrt(1/3)
setpw 1
setpc 0
;Kreis ============================
filled 7 [
arc 360 :r]
;Start im Center
;filled 4[
repeat 6[
pu fd :r rt 150+30*:dir pd
arc 60 :r ;stop
pu lt 150+30*:dir bk :r pd
rt 60*:dir ] ;stop
; Zusatz-Kreisbögen ========================
setpc (list (random 100)(random 100 )(random 100))
repeat 6[
repeat :anz-1 [
pu fd :r lt 60/:anz*repcount*:dir
bk :r lt 30+30*:dir pd
arc 60 :r ;===============================
pu rt 30+30*:dir fd :r
rt 60/:anz*repcount*:dir
bk :r pd ;stop
; Teil-Bogen fertig ;===============================
]
rt 360/6*:dir
]
End
to kreis.bogen.show
cs ht window
pu setxy -200 0 pd
kreis.boegen 400 50 pick [1 -1]
pu setxy 200 0 pd
kreis.boegen 400 50 pick [1 -1]
forever [
pu setxy (random -450 450) (random -300 300) pd
kreis.boegen (random 20 80) (random 20 30) pick [1 -1]
;wait 50
;cs
]
end
cs
;kreis.boegen 100 6 1
kreis.bogen.show
|
Kreiselkreise - Ergebnis
Die Kreiselkreise haben Zufallsfarben. Sie haben verschiedene Größen und Positionen. Sie sind mal nach rechts,
mal nach links gedreht.
Kein Bild ist wie das andere, denn alles wird jedesmal wieder frisch auf der Basis von Zufallszahlen erstellt.
Stellen Sie sich vor, Sie hätten alle diese Kreise per Hand zeichnen sollen - bloß das nicht!
Man sieht daran: Die kreative Denkarbeit steckt im Quell-Code - die Sklavenarbeit macht der Computer.
 Wenn man wenige Zeilen im Quellprogramm verändert, kann sich das Ergebnis schon stark verändern.
Ersetzen Sie doch mal die Zeilen
Wenn man wenige Zeilen im Quellprogramm verändert, kann sich das Ergebnis schon stark verändern.
Ersetzen Sie doch mal die Zeilen
setpc (list (random 100)(random 100 )(random 100))
repeat 6[
durch die Zeilen
make "hurz (random 1 6)
repeat 6[
setpc item (remainder :hurz+repcount 6)+1 [1 13 4 14 6 2]

|
|
Beispiel 2: Perfektes Quadrat
Ein "perfektes Quadrat" (auch: "quadriertes Quadrat") ist ein Quadrat, das sich vollständig in kleinere Quadrate aufteilen lässt,
wobei keine zwei dieser Teilquadrate einander gleich sein dürfen - oder, etwas mathematischer formuliert:
Ein Quadrat, das sich in lauter paarweise verschieden große Quadrate zerlegen lässt, heißt perfekt.
Lange war ungewiss, ob es überhaupt ein perfektes Quadrat gibt. Schließlich fand Roland Sprague eine Lösung mit 55
Quadraten. (Siehe hier)
1978 gelang es dem holländischen Mathematiker A.J.W.Duijvestijn auf der Basis eines 112x112-Quadrats, den Nachweis zu
erbringen, dass ein perfektes Quadrat auch mit 21 Teilen darstellbar ist. Die 21 Teilquadrate haben die Kantenlängen
2, 4, 6, 7, 8, 9, 11, 15, 16, 17, 18, 19, 24, 25, 27, 29, 33, 35, 37, 42 und 50. Oben haben wir 50, 35 und 27, unten 33, 37 und 42,
links 50, 29 und 33 und rechts 27, 19, 24 und 42. (Quelle: Ivan Moscovich, Formenrätsel, S. 65 ff. Weitere Infos
findet man unter dem Stichwort Quadratur_des_Quadrates.)
Das Perfekte Quadrat ist mit den LOGOtypischen Rechts-Links Befehlen programmiert worden. Das erscheint auf den
ersten Blick etwas plump. Es hat aber gegenüber der Verwendung von Koordinaten (was in JSLogo auch möglich ist)
den Riesen-Vorteil, dass man die Grafik vergrößern, in einem Winkel darstellen kann und deshalb gut in weiteren
LOGO-Programmen verwenden kann.
|
Perfektes Quadrat: Programm-Code
to quad.perf.show
forever [
cs
window
ht
seth pick [0 90 180 270]
pu setxy 0 40 pd
quad.perf 4
wait 150
]
End
to quad.perf :t
; From Center
pu fd :t*56 lt 90 fd :t*56 rt 90 pd
;pick [0 1 2 3 4 6 13 14]
; (list (random 100) (random 100) (random 100))
; Reihe oben
filled (list (random 100) (random 100) (random 100)) [quad :t*50]
;filled pick [0 1 2 3 4 6 13 14] [quad :t*50]
pu rt 90 fd :t*50 lt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*35]
pu rt 90 fd :t*35 lt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*27]
pu lt 90 fd :t*85 rt 90 pd
; Spalte links
pu bk :t*50 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*29]
pu bk :t*29 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*33]
; Reihe unten
pu rt 90 fd :t*33 lt 90 fd :t*4 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*37]
pu rt 90 fd :t*37 lt 90 fd :t*5 pd
filled pick [0 1 2 3 4 6 13 14] [quad :t*42]
; rechts nach oben
pu fd :t*18 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*18]
pu rt 90 fd :t*18 lt 90 fd :t*6 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*24]
pu fd :t*19 rt 90 fd :t*5 lt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*19]
pu lt 90 fd :t*8 rt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*8]
pu bk :t*8 lt 90 fd :t*3 rt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*11]
pu bk :t*11 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*6]
pu fd :t*11 lt 90 fd :t*17 rt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*17]
pu lt 90 fd :t*15 rt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*15]
pu bk :t*15 lt 90 fd :t*21 rt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*25]
pu bk :t*25 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*4]
pu rt 90 fd :t*25 lt 90 fd :t*16 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*16]
pu fd :t*9 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*9]
pu rt 90 fd :t*9 lt 90 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*2]
pu bk :t*2 pd
filled (list (random 100) (random 100) (random 100)) [quad :t*7]
pu rt 90 bk :t*63 lt 90 fd :t*52 pd
; To Center
pu rt 90 fd :t*56 lt 90 bk :t*56 pd
end
to quad :s
; Start ende oben links
repeat 4[
rt 90 fd :s ]
end
quad.perf.show
|
Perfektes Quadrat: Ergebnis

Möchten Sie ein Bild wie dieses selbst erzeugen?
- Den Quellcode links markieren und kopieren
- Die Seite JSLogo aufrufen
- Den Quellcode unten links einfügen
- Auf den Button "Run" drücken
- Auf Wunsch ein besonders hübsches Bild speichern über Extras-Download Drawing auf der rechten Bildschirm-Seite
Weiterentwicklung des Programms:
- Andere Farb-Kombinationen
- Das Programm viel eleganter programmieren
- Andere Flächen programmieren: Andere perfekte und unperfekte Quadrate oder perfekte und unperfekte Rechtecke
|
Beispiel 3: Tiling - Quadrat im Quadrat
In dem Rätselbuch "Die Sphinx" von Heinrich Hemme fand ich die Aufgabe "Das Quadrat im Quadrat" (S. 38). Sie lautet:
"Wenn man bei einem Quadrat die Ecken und die Seitenmittelpunkte miteinander verbindet, (...) entsteht in seinem
Inneren ein kleines Quadrat. In welchem Verhältnis stehen die Flächeninhalte des inneren und des äußeren Quadrats?"
Das Bild des Quadrats im Quadrat inspirierte mich zu folgender Aufgabe:
Wenn man eine beliebige Länge auf der Seite eines Quadrats entlanggeht und den erreichten Punkt mit der gegenüberliegenden
Ecke verbindet und dieses auf allen vier Seiten gleichermaßen tut, dann entsteht ein Innenquadrat. Ist der Punkt nur
wenig weit von der Ecke entfernt, so entsteht ein rel. großes Innenquadrat. Je näher er der Seitenmitte kommt, desto kleiner
wird das Innenquadrat.
Die Aufgabenstellung:
- Variable Größe der Innenquadrate
- Variable Farben der Teilflächen
- Mit diesen Zufalls-Quadraten eine Fläche parkettieren.
|
Programm-Code: Tiling - Quadrat im Quadrat
to quady :s :alpha :col1 :col2 :col3
make "beta 90-:alpha
make "gegen :s*(tan :alpha)
make "an2 :gegen*(cos :alpha)
make "gegen2 :gegen*(sin :alpha)
make "hyp sqrt(:s^2+:gegen^2)
; Große Dreiecke ========================
repeat 4[
filled :col1 [
fd :s rt 90
fd :gegen rt 90+:alpha
fd :hyp lt :alpha rt 180
fd :s rt 90]]
; Kleine Dreiecke ========================
repeat 4[
filled :col2 [
rt :alpha
fd :an2 lt 90
fd :gegen2 lt :alpha+90
fd :gegen rt 180
fd :s rt 90
]]
; Mittelquadrat ========================
rt :alpha fd :an2
filled :col3 [
repeat 4[
fd :hyp-:an2-:gegen2 rt 90]]
bk :an2 lt :alpha
end
to quady.tile :s :m :n
repeat :n [
repeat :m [
quady :s (random 4 44)
item (random 1 6) [1 13 4 14 6 2]
item (random 1 6) [1 13 4 14 6 2]
item (random 1 6) [1 13 4 14 6 2]
pu rt 90 fd :s lt 90 pd ]
pu lt 90 fd :s*:m rt 90
pu bk :s pd
]
end
cs
window
pu setxy -460 185 pd
quady.tile 100 9 5
;quady 200 25 4 1 2
|
Ergebnis: Tiling - Quadrat im Quadrat

Möchten Sie ein Bild wie dieses selbst erzeugen?
- Den Quellcode links markieren und kopieren
- Die Seite JSLogo aufrufen
- Den Quellcode unten links einfügen
- Auf den Button "Run" drücken
- Auf Wunsch ein besonders hübsches Bild speichern über Extras-Download Drawing auf der rechten Bildschirm-Seite
Ideen zur Weiterentwicklung des Programms:
- Bei Parkettierungen muss die Turtle jeweilse wieder an den Ausgangspunkt zurückkommen.
Das lässt sich viel eleganter lösen durch ein push-pop-Verfahren: Das Programm merkt sich die Koordinaten
des Ausgangspunktes und die Richtung der Turtle; Wenn die Turtle dahin zurückspringen soll, sagt man ihr das
über den Befehl setpos. Modifizieren Sie den Programmcode in dieser Weise!
- Nur wenige unterschiedliche Größen des Innenquadrats zulassen!
- Andere Farb-Kombinationen
- Innenquadrat wahlweise auch in die andere Richtung zeigen lassen
- Die Verbindung von Ecke zum Punkt auf der Seite in beide Richtungen nacheinander durchführen.
Dadurch entstehen innen ein Achtstern und ein Achteck. Und das Ganze noch in Farbe - ein Traum!
- Quadrate wahlweise mit anderen Mustern füllen
|
|
Beispiel 4: Unmögliches Objekt
|
Programm-Code: Unmögliches Objekt
to sexer :s
repeat 3[
; innen ======================
filled 4[
fd :s*4 rt 120
fd :s*3 rt 120
fd :s*1 rt 60
fd :s*1 lt 120
fd :s*2 lt 60
fd :s*2 lt 120
fd :s*1 rt 60
fd :s*1 rt 120
fd :s*3 rt 120
fd :s*4 rt 60]
; außen ===========================
pu rt 60 fd :s pd
filled 6[
fd :s*4 rt 120
fd :s*5 rt 60
fd :s*5 rt 120
fd :s*4 rt 120
fd :s*1 rt 60
fd :s*2 lt 120
fd :s*3 lt 60
fd :s*3 lt 120
fd :s*2 rt 60
fd :s*1 lt 60]
pu fd :s*1 rt 120 pd
; drei ==============================
pu rt 60 fd :s rt 60
fd :s lt 60 pd
fd :s rt 120
fd :s rt 120
fd :s
pu fd :s lt 60
fd :s rt 120 pd
rt 120]
end
cs
sexer 30
|
Ergebnis: Unmögliches Objekt

Möchten Sie ein Bild wie dieses selbst erzeugen?
- Den Quellcode links markieren und kopieren
- Die Seite JSLogo aufrufen
- Den Quellcode unten links einfügen
- Auf den Button "Run" drücken
- Auf Wunsch das Bild speichern über Extras-Download Drawing auf der rechten Bildschirm-Seite
Ideen zur Weiterentwicklung des Programms:
- Andere Farb-Kombinationen
- Eins der zwei kleinen Dreiecke ist nicht programmiert worden. Für welchen Zweck wäre es sinnvoll, dieses noch hinzuzufügen?
- Modifizieren Sie das Objekt so, dass es ein mögliches Objekt (ein Würfel) wird!
- Das Objekt hat die Grundform eines Sechsecks. Kacheln Sie eine Fläche mit solchen Sechsecken!
- Weitere unmögliche Objekte programmieren! Dazu "Unmögliche Objekte", "Impossible object", "Unmögliche Figuren" etc. googlen.
|
|
Beispiel 5: Sternen-Galaxie
|
Programm-Code: Sternen-Galaxie
to dreieck.gleichschenklig :alpha :hoehe
setpencolor "black
fd :hoehe / ( cos :alpha / 2 )
rt 180 - ( 90 - :alpha / 2 )
fd 2 * sqrt ( ( :hoehe / ( cos :alpha / 2 ) ) ^ 2 - :hoehe ^ 2 )
rt 180 - ( 90 - :alpha / 2 )
fd :hoehe / ( cos :alpha / 2 )
lt :alpha + 180
end
to drachen :alpha :hoehe1 :hoehe2
filled (list random 100 random 100 random 100)
[
dreieck.gleichschenklig :alpha :hoehe1]
fd :hoehe1 / ( cos :alpha / 2 )
rt 180 - ( 90 - :alpha / 2 ) - arctan :hoehe2 /
sqrt ( ( :hoehe1 / ( cos :alpha / 2 ) ) ^ 2 - :hoehe1 ^ 2 )
filled (list random 100 random 100 random 100)[
fd sqrt ( :hoehe2 ^ 2 + ( sqrt ( ( :hoehe1 /
( cos :alpha / 2 ) ) ^ 2 - :hoehe1 ^ 2 ) ) ^ 2 )
rt 2*arctan (:hoehe2 / sqrt ( ( :hoehe1 /
( cos :alpha / 2 ) ) ^ 2 - :hoehe1 ^ 2 ) )
fd sqrt ( :hoehe2 ^ 2 + ( sqrt ( ( :hoehe1 /
( cos :alpha / 2 ) ) ^ 2 - :hoehe1 ^ 2 ) ) ^ 2 )]
rt 180 - ( 90 - :alpha / 2 ) - arctan :hoehe2 /
sqrt ( ( :hoehe1 / ( cos :alpha / 2 ) ) ^ 2 - :hoehe1 ^ 2 )
fd :hoehe1 / ( cos :alpha / 2 )
rt 180-:alpha
end
to rotation :hoehe1 :hoehe2 :peaks
repeat :peaks [
drachen 360/:peaks :hoehe1 :hoehe2
rt 360/:peaks
]
hideturtle
end
to starshow
cs
window
setsc 9
forever [
pu setxy (random -600 600) (random -300 300) pd
rotation (random 10 50) (random 20 160) (random 5 30)
wait 50]
end
cs
;drachen 37 50 200
;rotation 50 125 19
starshow
;rotation (random 10 50) (random 20 125) (random 5 19)
|
Ergebnis: Sternen-Galaxie

Möchten Sie ein Bild wie dieses selbst erzeugen?
- Den Quellcode links markieren und kopieren
- Die Seite JSLogo aufrufen
- Den Quellcode unten links einfügen
- Auf den Button "Run" drücken
- Auf Wunsch das Bild speichern über Extras-Download Drawing auf der rechten Bildschirm-Seite
Ideen zur Weiterentwicklung des Programms:
- Andere Farb-Kombinationen
- Wenn die Sterne schneller erscheinen sollen, modifizieren Sie die Zeile "wait 50"! (z.B. wait 10 oder 0)
- Wie wäre es mit Sternen mit abgeknickten Zacken?
- Oder mit Sternen mit unterschiedlich langen Zacken?
- Statt Sternen können Blumen programmiert und eingesetzt (oder Sterne und Blumen) werden (siehe unten).
- Statt Sternen können Hypozykloide programmiert und eingesetzt werden.
Blumen-Feld

|
|
Beispiel 6: Durchlöcherter Würfel
|
Programm-Code: Durchlöcherter Würfel
to rom :s :dir
repeat 2[fd :s rt :dir*120 fd :s rt :dir*60]
end
to tres :s :dir
repeat 3[fd :s rt :dir*120]
end
to sierp.cube.2 :s :co1 :co2 :co3 :step
; Ausgang vom Center
repeat 3[
make "a 3*:s
filled :co1 [rom :a 1 ]
; Innen-Loch
pu fd :s rt 120 fd :s pd
make "a :s
filled :co2 [tres :a -1]
lt 60
filled :co3 [tres :a -1]
;back
pu lt -60 fd -:s rt -120 fd -:s pd
; Kleine Innen-Löcher 1
pu fd :s/3 rt 120 fd :s/3 pd
filled :co2 [tres :a/3 -1]
lt 60
filled :co3 [tres :a/3 -1]
;back
pu lt -60 fd -:s/3 rt -120 fd -:s/3 pd
; Kleine Innen-Löcher 2
pu fd :s/3*7 rt 120 fd :s/3 pd
filled :co3 [rom (:s/3) -1]
lt 60
;back
pu lt -60 fd -:s/3 rt -120 fd -:s/3*7 pd
; Kleine Innen-Löcher 3
pu fd :s/3 rt 120 fd :s/3*7 pd
filled :co2 [rom (:s/3) -1] ;
lt 60
pu lt -60 fd -:s/3*7 rt -120 fd -:s/3 pd
; Kleine Innen-Löcher 4
pu fd :s/3*7 rt 120 fd :s/3*7 pd
filled :co2 [tres :a/3 -1]
lt 60
filled :co3 [tres :a/3 -1]
;back
pu lt -60 fd -:s/3*7 rt -120 fd -:s/3*7 pd
;=============
rt 120
make "co4 :co2 ; Hilfsspeicher
make "co2 :co1
make "co1 :co3
make "co3 :co4
]
End
cs
ht
rt 60
;rom 50 1
sierp.cube.2 50 2 6 4 1
;sierp.cube.2 50 2 6 13 14
|
Ergebnis: Durchlöcherter Würfel
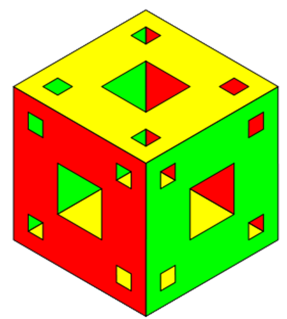
Möchten Sie ein Bild wie dieses selbst erzeugen?
- Den Quellcode links markieren und kopieren
- Die Seite JSLogo aufrufen
- Den Quellcode unten links einfügen
- Auf den Button "Run" drücken
- Auf Wunsch das Bild speichern über Extras-Download Drawing auf der rechten Bildschirm-Seite
Ideen zur Weiterentwicklung des Programms:
- Würfel anders einfärben
- 8 statt 4 kleine Löcher
- Statt 4 kleiner Löcher 2 L-förmige Löcher
- Statt der quadratischen Löcher sternförmige Löcher aus jeweils 5 Quadraten
- Aus dem Würfel einen 2x2x2 Würfel konstruieren!
|
|
LOGO lernen von der Pike auf
Es gibt ausreichend Einführungen in Logo. Denen muss ich nicht noch eine weitere hinzufügen.
Es genügt, auf ausgewählte Einführungen zu verlinken.
|
Links zum LOGO Lernen von der Pike auf
|
Tipps zum Programmieren
- Programmcode mit Kommentaren versehen. Sie werden einfach durch ein Semikolon eingeleitet.
Man kann sie auch gebrauchen, wenn man das Programm strukturieren möchte durch z.B. Striche.
Auch praktisch, wenn man einen Teil nur vorläufig unterdrücken möchte.
- Zum Fehler-Finden (Debuggen) ist das Einfügen von STOP praktisch. Dann findet man leichter, an welcher Stelle etwas
schiefläuft. Eventuell hilft es auch, wait 100 einzufügen, so dass das Programm langsam abläuft.
|
Eine LOGO-Seite mit Appetithäppchen von Volker Pöhls
Möchten Sie den Webmaster freundlich kontaktieren?
Mail an den Webmaster
First published: 08.04.2019
Last Update: 06.05.2020
|
Andere Angebote vom selben Autor:
|
|
|